Physical blog

   Merev testről beszélünk, ha a test a rá ható erők hatására elhanyagolható mértékő
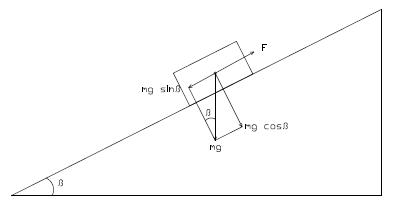
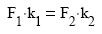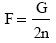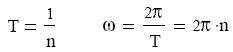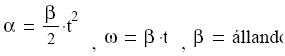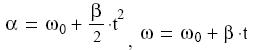alakváltozást szenved. Bármely két pontja közötti távolság állandó marad.
A merev testet érő hatás nemcsak az irányától és a nagyságától függ, hanem hogy, hogy
hat a testre. Ezért fontos ismernünk az erő hatásvonalát és támadáspontját.

Erő hatásvonala: Az az egyenes, amely mentén az erővektor hat, az erő
hatásvonalának nevezzük.

Támadáspont: Az a pont, ahol az erőhatás a testet éri, az erő támadáspontja. Az erő
támadáspontja a hatásvonala mentén eltolható.

Tapasztalatból tudjuk, hogy amennyiben a testre egy olyan erő hat, amelynek
hatásvonala nem megy át a tengelyen, a test gyorsulva forogni kezd. Ez a jelenség a
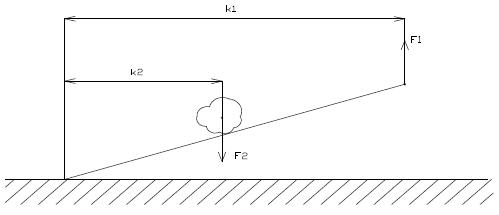
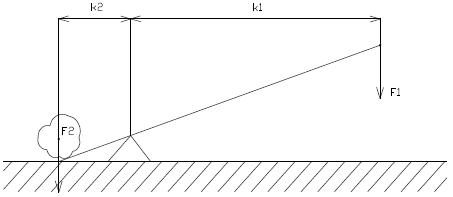
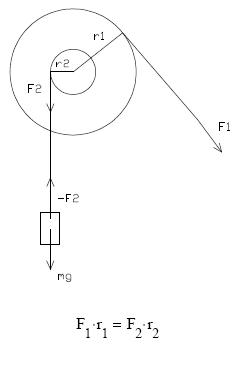
forgatónyomaték, amely az erı és erőkar szorzata kapunk.

Erőkar: Az erő hatásvonalának a tengelytől mért távolsága az erőkar.

Forgatónyomaték: Az erő adott tengelyre vonatkozó forgatónyomatéka az erő
nagyságának és az erőkarnak a szorzata.
                                                 M=F×x
ahol M a forgatónyomaték, F az erő és x az erőkar. Mértékegysége: Nm.

Merev test egyensúlyának feltétele: A rá ható erők eredője és az erők valamely pontra
vonatkozó forgatónyomatékainak összege nulla legyen. Ha az eredő nem nulla, a test
gyorsul. Ha a forgatónyomaték-összeg nem nulla, a test gyorsuló forgást végez.



Csak olyan eseteket tárgyalunk, amelyekben a merev testre ható erők egy síkban hatnak.























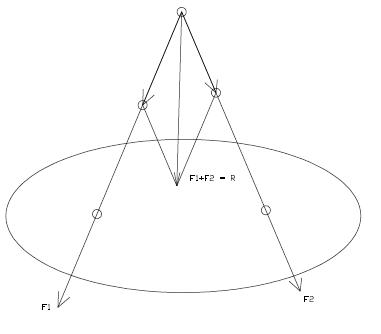
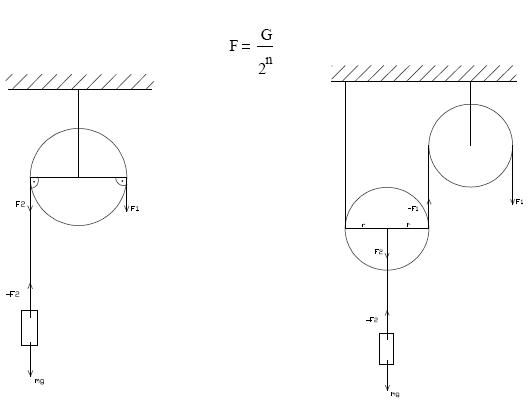
Szöget bezáró erők összege: Az ábra látható az F1 és F2 erő melyek nem
párhuzamosak egymással. Támadáspontjukat eltolhatjuk hatásvonalaik metszéspontjába,
így már összegezhetjük őket. Az erők eredıjét szintén eltolhatjuk a hatásvonaluk mentén.
Ez akkor fontos, ha a hatásvonalaik metszéspontja a testen kívül van.

Erőpár : A párhuzamos hatásvonalú, ellentétes irányú, egyenlőnagyságú erő neve az
erőpár.

Az erőpár forgatónyomatéka a forgástengely helyétől függetlenül M=Fxd, ahol F az erők
nagysága, d pedig a hatásvonalaik távolsága. Megállapítható, hogy egy erőpárt
legegyszerűbben egy másik erőpárral tudjuk kiegyensúlyozni.

Ha egy merev testet egyensúlyi helyzetéből kimozdítunk, az új helyzetben az eredő és a
forgatónyomaték általában nem nulla. Ha ebben a helyzetben a testet magára hagyjuk,
három dolog lehetséges. A test visszatér egyensúlyi helyzetébe, új egyensúlyi helyzet
elérésére törekszik, vagy abban a helyzetben marad, amelybe elmozdítottuk.


Egyensúlyi helyzetek :

Stabil: Azt az egyensúlyi helyzetet, amelybe a test kismértékő kimozdítása után
visszatér.

Labilis (bizonytalan): Azt az egyensúlyi helyzetet, amelyből a testet bármilyen kis
mértékben kimozdítva, a test tovább mozog, új egyensúlyi helyzet elérésére törekedve,
labilis egyensúlyi helyzetnek nevezzük.

Közömbös (indifferens): Az az egyensúlyi helyzet, amelyből testet bármilyen
mértékben kimozdítva, a test új helyzetében szintén egyensúlyi helyzetben lesz.

Egyszerű gép, például az emelő, a hengerkerék, csigák és csigasorok, valamint a lejtő
típusú szerkezetek.

Az emelő olyan merev test, amely egy tengely körül foroghat. Két fajtája az egykarú
és a kétkarú emelő.













Mindkét típusra teljesül, hogy az erők tengelyre vonatkozó forgatónyomatékának
összege nulla. Egyenlettel kifejezve:



A hengerkerék a kétkarú emelő speciális esete. Az emelőkkel csak kis magasságú
emelések végezhetők, míg a hengerkerék folyamatos munkavégzést tesz lehetővé.
Alkalmazása esetén az F1 emelőerő az r1 sugarú kerék érintőjének, míg a teher által
kifejtett F2 erő kerékkel közös tengelyen lévő r2 sugarú henger érintőjének irányába
mutat. Az egyenletes emeléshez szükséges, hogy az F2 és az m·g nehézségi erő nagysága
egyenlő legyen, és az F1, F2 erő forgatónyomatékai megegyezzenek:

Hengerkerék, például a kerékpár pedálja, a daráló karja, a kerekes kút, stb.

Csigák és csigasorok: Az állócsiga arra való, hogy az erő irányát megváltoztassuk. Az
F1 és F2 forgatónyomatékának a csiga tengelyére egyenlőnek kell lennie. Mivel a két erő
karja egyenlő, a két erő nagysága megegyezik. ( ábra).

A mozgócsiga esetében a testet két kötél tartja, így egy-egy kötélben csak a teher
nagyságának a fele ébred. (ábra). Így közönséges csigasornál, ha 2n az álló- és
mozgócsigák száma (2n=egy mozgó + egy álló):




Arkhimédészi csigasor esetében n db mozgó csiga alkalmazása esetén  (ábra):
















































A lejtő alkalmazásakor a testet általában vagy a lejtővel, vagy a lejtő alapjával
párhuzamos erővel mozgatjuk. (ábra)














Ha megvizsgáljuk az óriáskerék egy fülkéjének a mozgását, azt tapasztaljuk, hogy a
fülke minden pontja körpályán mozog. az egyes pontok pályája egymással egybevágó. A
mozgás során minden pont sebessége ugyanakkora, és a test térbeli iránya nem változik.
A merev test ilyen mozgását transzlációnak nevezzük.

Transzláció (eltolás, haladó mozgás): A merev test olyan mozgása, amely során a
testen kijelölt két, nem párhuzamos egyenes-szakasz eredeti helyzetével mindvégig
párhuzamos marad. A transzláció jellemezhető egyetlen (d)r vektorra (a test bármely
pontjának elmozdulásvektorával).

Ugyanakkor, ha megfigyeljük a lemezlejátszó korongjának mozgását, azt tapasztaljuk,
hogy minden pontja körpályán mozog. Az egyes pontok pályájának sugara különböző lehet,
de minden egyes pont ugyanazon tengely körül forog. Ez a forgómozgás a rotáció, ami egy fix tengely körüli mozgás.

Tehát a merev testek folytathatnak haladó mozgást, foroghatnak egy rögzített tengely
körül, valamint végezhetnek egyszerre haladó és forgó mozgást.

  Egyenletes forgómozgás esetén a test szögelfordulása arányos a szögelfordulás idejével.
Egyenlettel kifejezve: (delta alfa) = w×(delta)t, ahol (delta alfa) a szögelfordulás, (delta)t a szögelfordulás ideje, w pedig a szögsebesség. Egyenletes forgómozgást végez, például a lemezlejátszó korongja. A forgó merev test minden pontja körmozgást végez és sebessége a v= (omega)×r összefüggéssel adható meg. Érzékelhető, hogy minél távolabb megyünk forgástengelytől, az elemi részecskék sebessége egyre nagyobb lesz. Ezért a forgómozgás leírására a sebesség nem alkalmas, ezért helyette a szögsebességet használjuk. Használjuk még a periódusidőt, amit T-vel jelölünk, valamint a fordulatszámot, ami a periódusidő reciproka (jele: n, vagy f.).




Egyenletesen változó forgómozgás esetében a szögelfordulás a forgástengely körül
időben változó lesz, mégpedig úgy, hogy az éppen az idő négyzetével lesz arányos. Az
arányossági tényezıt β-val jelöljük, és szöggyorsulásnak hívjuk. Dimenziója: 1/idő a
négyzeten, mértékegysége: 1/s². Abban az esetben, ha a test álló helyzetből indul, az
egyenletesen változó forgómozgást leíró összefüggések a következık:





H a időmérés kezdetén a test már forgott (van kezdő szögsebessége),

   Abban az esetben, ha a test egyes pontjai mozgásuk során egy síkban maradnak, és ezek
a síkok egybeesnek vagy párhuzamosak, akkor síkmozgásról beszélünk. Matematikailag
kifejezve úgy is értelmezhetnénk, hogy a merev test x, y, z koordinátatengelyei közül csak
egy tengelyen történik mozgás. Ilyen síkmozgás például a guruló labda, vagy a gépjármű
kereke. Mozgó jármű esetében, csúszásmentes gördülést feltételezve a kerék tengelymenti
’v’ sebessége megegyezik a kerék szélső pontjainak sebességével. Ebből az is következik,
hogy a tengely gyorsulása és a kerék szélső pontjainak kerületi gyorsulása is megegyezik.
Egyenlettel kifejezve:

   A merev testre ható forgatónyomaték és az általa létrehozott szöggyorsulás egyenesen
arányos. Egyenlettel:    

     

ahol Θ a forgó test forgási tehetetlensége, amit tehetetlenségi nyomatéknak hívunk.
Dimenziója: tömeg szorozva a távolság négyzetével.
Mértékegysége: kgm².  

Ebből látszik, hogy a tehetetlenségi nyomaték értéke a tengely helyétől is függ, azaz egy
testnek különböző nagyságú lehet a tehetetlenségi nyomatéka attól függően, hogy a tengelyt mely ponton választjuk ki. A tömegpont választása esetén a távolság, éppen a tömegponttól mért távolság lesz. Egyéb esetekben úgy számolhatjuk ki a tehetetlenségi nyomatékot, hogy a testet olyan darabokra bontjuk, amelyek már pontszerűnek tekinthetők, és az ezekre számított tehetetlenségi nyomatékok összegét számoljuk. A tehetetlenségi nyomaték meghatározását segíti a Steiner-tétel, miszerint ha ismert az m tömegű test tömegközépponti tehetetlenségi nyomatéka valamely átmenő tengelyre, akkor a vele párhuzamos, tőle s távolságban lévő tengelyre a tehetetlenségi nyomaték: