Ha egy fémtestre töltést viszünk, akkor a test potenciálja a rávitt töltéssel arányosan nő, feltéve, hogy a fémtest környezete közben nem változik. A magányos vezetıőre jellemző a rávitt töltés és a létrejött potenciál hányadosa, neve: töltésbefogadó képesség, vagy kapacitás, jele: C, mértékegysége a farad, F.   C = Q/U.

Egy r sugarú vezetıgömb kapacitását könnyen meghatározhatjuk: C = Q/U = Q/kQ/r =
r/k.

Kondenzátor (sűrítő): Olyan berendezés, melynek célja, hogy minél kisebb térrészben
minél több töltést tároljon, minél kisebb feszültségen, vagyis minél nagyobb legyen a
kapacitása.

Síkkondenzátorok: Két nagy felülető, egymással párhuzamos, egymáshoz közel
helyezett sík fémlemez.

A síkkondenzátor lényegében két azonos kiterjedésű párhuzamos fémlemez, amelyeket
+Q és –Q töltéssel látunk el. A két lemez három tartományra bontja a teret. Az egyes
lemezektől származó térerősségek a két szélső tartományban ellentétes irányúak, ezért ott az összegük nulla, a középső tartományban pedig azonos irányúak, így az összegük:




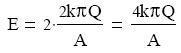
Ha a lemezek távolsága d, akkor a feszültség:




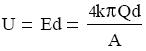
így a kapacitás





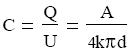
A síkkondenzátorok kapacitása tehát egyenesen arányos a felülettel, és fordítottan
arányos a lemezek távolságával.


Kondenzátorok kapcsolása: Soros kapcsolás.







 
Kapcsoljunk össze két kondenzátort úgy, hogy fémesen összekötjük egy-egy lemezüket,
más néven fegyverzetüket. (ábra). Az így kapott közös pont, a B pont. Ha +Q töltést
adunk az A felőli lemeznek, és a C pontot leföldeljük, akkor a két kondenzátor a megosztás
révén azonos töltésre töltődik. A feszültség A és C között a két kondenzátor feszültségének összege, azaz U = U(alsó index:AC) = U(alsó indexAB) + U(alsó indexBC).

A kondenzátorrendszer Q töltést tárol. A rendszer helyettesíthető olyan C kapacitású
kondenzátorral, amelyen Q töltés szintén U feszültséget hoz létre. Felhasználva, hogy U =
Q/C, a feszültségre az alábbi összefüggés írható fel.




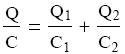
A kifejezést Q-val egyszerősítve megkapjuk a soros kapcsolású
kondenzátorok eredı kapacitására vonatkozó összefüggést:





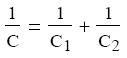
Sorosan kapcsolt kondenzátorok esetén az eredő kapacitás reciproka az egyes
kapacitások reciprokainak összege.

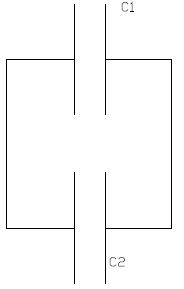
Párhuzamos kapcsolás: Kapcsoljunk össze két kondenzátort úgy, hogy fegyverzeteiket
páronként összekötjük, és vigyünk fel a rendszerre Q töltést . A helyettesítő kondenzátor C kapacitása a következőképpen határozható meg. A kondenzátorok feszültsége azonos kell hogy legyen, úgy, hogy a helyettesítő kondenzátor töltés egyenlő a párhuzamosan
kapcsolt kondenzátorokon tárolt töltések összegével.



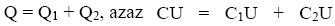
A közös feszültséggel osztva, a párhuzamosan kapcsolt
kondenzátorok eredő kapacitását kapjuk:


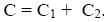
A párhuzamosan kapcsolt kondenzátorok kapacitásai összeadódnak.





















A kondenzátor energiája: Legyen egy adott pillanatban a lemezek közti fezsültség U,
és egy (delta)Q töltést vigyünk át a kondenzátor egyik fegyverzetérıl a másikra a már kialakult elektrosztatikus tér ellenében. Ekkor a töltés átviteléhez szükséges munka:
(delta) W = U ·(delta)Q.

Az U feszültség eléréséhez szükséges összes munka, pedig




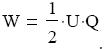
A képlet a kondenzátor kapacitásának felhasználásával átírható.





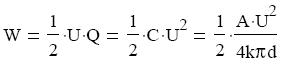
Ezt a térerősséggel kifejezve:





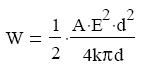
Ha egyszerősítünk d-vel és elosztjuk az oldalakat a kondenzátor térfogatával,





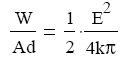
amit tovább egyszerősítünk két új fogalom bevezetésével. Az ω = W/Ad mennyiség az
egységnyi térfogatban található energia, azaz az elektrosztatikus tér energiasőrősége. Az
1/4πk = ε(alsó index:0) azaz a vákuum dielektromos állandó behelyettesítésével:






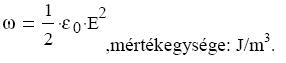
Kondenzátor szigetelőkkel: Töltsünk fel egy kondenzátort Q töltéssel, majd tegyünk
lemezei közé egy szigetelő üveglapot. Azt tapasztaljuk, hogy a feszültség csökken. Ha az
üveglapot eltávolítjuk, akkor a feszültség az eredeti értékére áll vissza, azaz a kondenzátor töltése nem változott meg. A jelenséget azzal magyarázhatjuk, hogy a szigetelıanyag behelyezésével megváltozik a kondenzátor kapacitása. Mivel a feszültség változatlan töltés mellett csökkent, a kapacitás megnőtt. Megállapodás szerint az
ε(alsó index:r) = C/C(alsó index:0) hányados értékét, ami csak a behelyezett szigetelőanyagra jellemző, az anyag relatív permittivitásának
nevezzük. Számértéke megmutatja, hogy hányszorosára nő a kondenzátor kapacitása az üres kondenzátoréhoz képes.