Physical blog

   A merev test mozgási energiájának megváltozása megegyezik az egyes tömegpontokra
ható erő munkájának összegével.






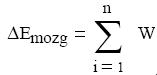
A külső és belső erők munkáját külön összegezve. A belső erők összege azonban most
nulla. Két szomszédos részecske elmozdulása megegyezik egymással, az erők úgyanakkora
nagyságúak, de ellentétes irányúak, így az összegük nulla.

Tehát egy merev test mozgási energiájának megváltozása megegyezik a testre ható
(külső) erők munkájának összegével.





Ha azonban az egyes sebességeket a v = r · ω összefüggés alapján fejezzük ki,













Tehát a forgási energia:

  A forgó test tehetetlenségi nyomatékának és szögsebességének a szorzata.
(impulzusmomentuma): N = Θ·ω . Jele: N, mértékegysége: kg · m²/ s .
A perdülettel megfogalmazható a forgómozgás alaptörvénye:




Látható, hogy abban az esetben, ha M = 0, akkor (delta)N = 0. Ezt a következő tétel
fogalmazza meg: Ha a külső forgatónyomatékok összege nulla, a test perdülete állandó. Ez
a perdület megmaradásának tétele.

   Minden test megmarad a nyugalom vagy az egyenes vonalú egyenletes mozgás
állapotában mindaddig, amíg valamilyen erőhatás ennek elhagyására nem kényszeríti. A
testeknek az a tulajdonsága, hogy mozgásállapotuk csak erı hatására változik meg, a testek
tehetetlensége. Az olyan vonatkoztatási rendszereket, amelyekben teljesül a tehetetlenség
törvénye, inercia-rendszernek nevezzük.

   A tömegpontot a fellépő erő saját irányába gyorsítja, az így létrejövő gyorsulás
egyenesen arányos az erővel. A testre ható erő és a gyorsulás hányadosát a test tehetetlen
tömegének nevezzük egyenlettel megfogalmazva:
                                              F = ma
mértékegysége: kg m/s² = N. A tömegpontra ható erők eredője egyenlő a test tömegének
és gyorsulásának szorzatával.

   Ha az egyik test erőt fejt ki a másikra, a másik is erőt fejt ki az előzıre, tehát az erők
mindig párosával lépnek fel. Ezek az erők egyenlő nagyságúak és ellentétes irányúak.

Súly és súlytalanság: Newton I. tv –ből a már ismert képletet segítségül hívva (F= ma, és behelyettesítve g nehézségi gyorsulást, megkapjuk egy test súlyát. G = mg.

Ha egy test a súlytalanság állapotába kerül, G = 0. Mivel a tömege nem változik a
testnek, így a gyorsulásnak kell 0-nak lennie. Tehát ha egy test szabadon esik, akkor
súlytalanság állapotába kerül. G = m(g – a), ahol a = g.

Súrlódási jelenségek: A csúszási súrlódási erı két egymással érintkező, egymáshoz
képest mozgó felület között lép fel. Iránya ellentétes a relatív sebességek irányával,
nagysága a felületek simaságától és az őket összenyomó erı nagyságától függ. A felületek
simaságát az úgynevezett súrlódási együtthatóval jellemezzük, jele: μ, ami dimenzió nélküli
mennyiség.



A tapadási súrlódási erő két egymással érintkező, egymáshoz képest nyugvó felület
között lép fel abban az esetben, ha valamilyen erı a felületeket el akarja mozdítani. A
tapadási súrlódási erő kényszererő. Jele:




Az impulzus: Ha egy test sebességét a rá ható erők t idő alatt v-ről v’-re változtatják, a
gyorsulás definíciója és a dinamika alapegyenlete miatt felírhatók a következők:









Az F(delta)t szorzatot erőlökésnek, az mv szorzatot impulzusnak (lendület) nevezzük. Az impulzus jele I, vagy p. Mértékegysége: kgm/s. Előző egyenletünket az impulzussal felírva:


képlethez jutunk.

A test időben változó impulzusa egyenlő az őt érő erőlökéssel. Ez az impulzustétel, ami
Newton II. törvényének egy másik megfogalmazása.