Physical blog

   Az optikai jelenségek nagyon jól magyarázhatók a Huygens-Fresnel-elv alapján,
miszerint a fény hullámtermészető, így minden nehézség nélkül leírható a hullámelmélet
alapján. Ezek ellenére azt a közelítést használjuk, hogy a fény frekvenciája nagyon nagy, így hullámhossza nagyon kicsi, homogén közegben, egyenes vonalban terjed, nem vesszük
figyelembe az elhajlást, ill. az interferenciát.
A fény két közeg határfelületére érve megváltoztatja terjedési irányát, egy része átlép a
másik közegbe, másik része visszaverıdik. E két, mindig egyszerre fellépı jelenség
fogalmazódik meg a visszaverıdés, ill. a törés törvényében.

A beesési szöge a beeső sugárnak a beesési merőlegessel bezárt szöge.
A visszaverődés szöge a visszavert sugárnak a beesési merılegessel bezárt szöge.
A törés szöge a megtört sugárnak a beesési merőlegessel bezárt szöge.
A visszaverődés törvénye szerint a beeső fénysugár, a visszavert fénysugár és a beesési merıleges egy síkban vannak.

A beesési szög megegyezik a visszaverıdés szögével.
A törvényből közvetlenül következik, hogy ha sík felületre párhuzamos nyaláb érkezik,
akkor az párhuzamosan is verődik vissza. Amennyiben a fény nem sík felületre érkezik,
hanem ott apróbb egyenetlenségek vannak, a fény minden irányba szétszóródik. Ez a diffúz visszaverődés jelensége.
A törés törvénye szerint a beeső fénysugár, a megtört fénysugár és a beesési merőleges
is egy síkban vannak. A beesési szög szinusza arányos a törési szög szinuszával. Az arányossági tényező az ún. relatív törésmutató (Snellius-Descartes-törvény):





ahol α a beesési szög, β pedig a törés szöge, n21 pedig a második közegnek az elsőre
vonatkozó törésmutatója.
Nyilvánvaló, hogy fordított irányú átmenet esetén ennek reciprokát kapjuk. Ha a fény
vákuumból lép az illetı anyagba, akkor abszolút törésmutatóról beszélünk.

A visszaverődés és törés speciális problémái

Visszaverődé gömbfelületről
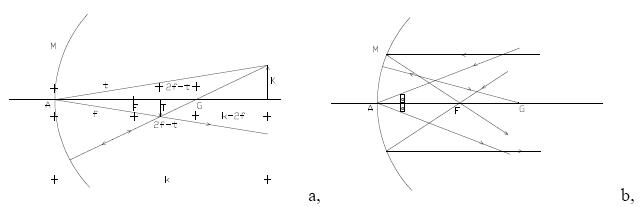
Az a pont, ahova a homorú tükör a rá eső párhuzamos nyalábot összegyőjti (optikai
tengelyen), ill. ahonnan a domború tükör által szétszórt nyaláb kiindulni látszik, a
fókuszpont, Jele: F.
Az ábráról leolvasható, hogy MFG háromszög, ahol G a tükör görbületi középpontja, és
M a fény és tükör találkozásának helye, egyenlőszárú háromszöget alkot. Az MG szakasz
éppen a kör sugara, így:





Ha β kicsi, akkor a cosβ értéke 1, így FG = R/2 , ezért AF = f = R/2.
Látható, hogy ha nagy a tükör nyílásszöge, akkor a tengelytől távolabb beeső sugarak
jóval közelebb metszik az optikai tengelyt, mint a közeliek. Ez persze akkor áll fenn, ha a
sugarak párhuzamosak az optikai tengellyel. Az ebből származó leképezési hibát gömbi (
szférikus) hibának nevezzük.




Fény áthaladása párhuzamos síklapokkal határolt optikai törıközegen (plánparalel lemez)
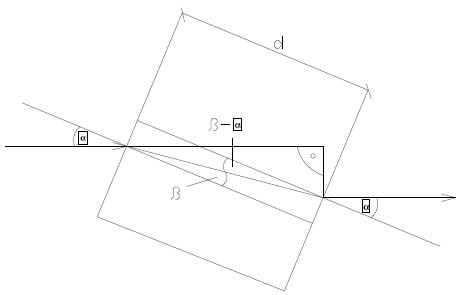
Ha fénysugarat bocsátunk egy d vastagságú, n törésmutatójú üveglemezre, azt
tapasztaljuk, hogy a kétszeri törés után az eredetivel párhuzamos irányban halad tovább a
sugár, csak egy kicsit eltolódott. Számítsuk ki az eltolódás nagyságát.

























Fény áthaladása egymással szöget bezáró síklapokkal határolt optikai törıközegen
(prizma)
Bocsássunk prizmára egy fénysugarat. A Két síklap szöge Φ, ez a prizma törıszöge.
Legyen a beesési szög α1. A fény mind belépésnél, mind kilépésnél megtörik. A  ábra
szerint a teljes eltérítés szöge δ = α1 + α2 – Φ.
Számítások szerint a minimális eltérítés szögét akkor kapjuk, amikor a sugármenet
szimmetrikus. δ = 2α – Φ.
Ekkor a Φ törıszög és a minimális δ eltérítési szög között a következı összefüggés áll
fenn:






















Fény áthaladása gömbfelületekkel határolt optikai törıközegen (lencse)
Legyen egy kétszer domború lencse két gömbfelületi görbületi sugara R1, ill. R2 ,
anyagának törésmutatója n. Ekkor a fókusztávolság reciproka:

   Valódi a kép, ha ernyőn felfogható, vagyis a fénysugarak összetartóak. Látszólagos a
kép, ha a leképező eszközt elhagyó sugárnyaláb széttartó, a képet a sugarak
meghosszabbításában látjuk.
Gömbfelülető lencsék és tükrök esetén nem tökéletesen valósul meg az optikai
leképezés, de kis nyílásszögő tükrök, ill. vékony lencsék esetén nagyon kicsi a leképezés
hibája.

Sík tükör
Sík tükrök esetén a látszólagos kép megegyezik az eredetivel, és azonos távolságban
látszik.

Homorú tükör
Optikai padra helyezzünk homorú tükröt, egy égő gyertyát és egy ernyőt. A gyertya
tologatásával keressük meg a gyertya lángjának éles képét az ernyn. ( ábra a,)
A következő nevezetes szerkesztővonalakat használhatjuk (ábra b,):
- a fókuszon átmenő sugarat, amely visszaverıdés után párhuzamos az optikai
tengellyel;
- az optikai tengellyel párhuzamos sugarat, amely visszaverıdés után átmegy a
fókuszon;
- a geometriai középponton átmenı sugarat, amely önmagába verıdik vissza;
- a tükör középpontjába irányított sugarat, amely az optikai tengellyel szimmetrikusan
verıdik vissza.




Az ábrán látható (felső ábra) két hasonló háromszög: K : T = k : t, illetve
K : T = (k – 2f) : ( 2f – t).
A kettőt egybevetve kapjuk a leképezési törvényt:




Teljesen hasonló módon lehet domború tükörre is levezetni a leképezési törvényt.
Nagyításnak nevezzük az előjelesen vett képtávolság és tárgytávolság arányát.
N = k / t = f / t - f.
Negatív a nagyítás értéke, ha 0 < t < f.
Ha f < t < 2f , akkor a kép nagyított és fordított állású, ill. valódi.
Ha 2f < t, akkor a keletkező kép kicsinyített, fordított állású, valódi
Ha f = t, akkor nem keletkezik kép, a fókuszból induló sugarak a tükörrıl visszaverődve
párhuzamosan haladnak.
Optikai padra helyezünk egy domború lencsét, egy égı gyertyát, és egy ernyőt. A
gyertya tologatásával keressük meg a gyertya lángjának éles képét az ernyőn.
A következő nevezetes szerkesztéseket hajthatjuk végre ( ábra):
- a fókuszon átmenı sugarat, amely törés után párhuzamos az optikai tengellyel;
- az optikai tengellyel párhuzamos sugarat, amely törés után átmegy a fókuszon;
- a lencse középpontjába irányított sugarat, amely törés nélkül halad tovább.



Az ábrán látható két hasonló háromszögre felírhatjuk, hogy:
K : T = k : t, illetve K : T = (k – f) : f.
A kettőt egybevetve a leképezési törvényt kapjuk:




A homorú tükör lépalkotásával teljesen analóg módon vezethetjük be a nagyítást.
N = k / t = f / t – f.
- Negatív a nagyítás értéke, ha 0 < t < f, ekkor a kép egyenes állású, nagyított.
- Ha f < t < 2f, akkor a keletkezı kép nagyított fordított állású, valódi.
- Ha 2f < t, akkor a keletkező kép kicsinyített, fordított állású, valódi.

   Az ókori görögöknél Démokritosz képzelte el elıször az atom létezését (atom-görögül
oszthatatlant jelent). Igazán hatásos elırelépést a kémia tett az atomelmélet kialakulásában a XVIII. század végén, XIX. század elején. Lavoisier már tisztázta az elemek fogalmát, és arányát a vegyületekben, majd Proust felállította az állandó súlyviszonyok törvényét:
A kémiai elemek nem egyesíthetık vegyületekké bármilyen arányban, hanem csak egy, a
vegyületre jellemzı súlyarány szerint.
Röviddel utána Dalton megfogalmazta a többszörös súlyviszonyok törvényét (1803):
Ha két elem többféle arányban is képes egymással vegyülni, akkor az egyik elem azon
mennyiségei, amelyek a másik elem egy adott mennyiségével vegyülnek, úgy viszonylanak
egymáshoz, mint a kis egész számok.
Eszerint tehát minden egyes elem atomjai azonosak, és a molekulák kisszámú különbözı atomokból állnak. A reagáló gázok térfogatarányai között hasonló törvény fogalmazható meg. Ezután született meg Avogadro törvénye: Azonos nyomás, térfogat és hımérséklet mellett a gázok azonos számú részecskéket tartalmaznak.
A molnyi mennyiségben lévı molekulák száma, amit több módszerrel is meghatároztak:
N = 6,02 · 1023 .
Bevezették az atomsúly és a molekulasúly fogalmát, amiket mai szóhasználattal relatív
atom-, illetve molekulatömegnek nevezünk. Meggyızı bizonyítéknak számított az atomok és
molekulák létezésére az Einstein által értelmezet Brown-mozgás: Ha mikroszkóppal
figyelünk füstszemcséket levegıben, vagy apró festékszemcséket folyadék felszínén, akkor
azok rendezetlen, zegzugos mozgását tapasztaljuk. Brown elıször virágporszemcsék
mozgását észlelte mikroszkópjában, 1827-ben.

  Az elektrolízis

Elektrolitoknak nevezzük a savak, lúgok, sók oldatait vagy olvadékait, mivel ezek
vezetik az áramot, ellentétben például a tiszta vízzel.
Ha elektrolitba helyezünk két elektródát, amiket egy külsı áramforrásra kötünk. A
körben mérhetı az áramerısség, melynek ismeretében megkapjuk az elszállított töltés
nagyságát. Az áram az ionok vándorlásának következménye: az ellentétes elıjelő töltéssel
rendelkezı ionok különbözı elektródákhoz vándorolnak, semlegesítıdnek, s ott általában gáz,
vagy szilárd halmazállapotban kiválnak.
A kinyert anyagok mennyisége, és így az ionok darabszáma kémiai mérésekkel
határozható meg.





Ahol qion egy ion töltése, Q a szállított össztöltés, amelyet I áram t idı alatt szállít, és
Nion az ionok darabszáma.

Ugyanerre az eredményre vezettek Faraday elektrolízissel kapcsolatos tapasztalati
törvényei is.
I áramerıség mellett, t idı alatt az elektródákon levált anyag tömege m = k I t, ahol k az
elektrokémiai egyenérték, amely az egységnyi töltés által kiválasztott anyag tömegét jelenti, vagyis az elektrokémiai egyenérték az anyag minıségétıl függı állandó.
Egy molnyi anyag kiválasztásához annyiszor 96 500 C töltés szükséges, amennyi az
illetı anyag vegyértéke. A két törvény és az Avogadro-szám ismeretében az egy vegyértékő anyag egy ionjára jutó töltés:






A Millikan –kísérlet
Millika angol fizikus vízszintesen elhelyezett kondenzátorlemezek közé olajcseppeket
porlasztott, majd ezeket mikroszkópon keresztül figyelte meg. Egy olajcseppet kiválasztva
addig változtatta az elektromos mezıt, amíg az olajcsepp lebegni nem kezdett, és a gravitációs erő ellenében az elektrosztatikus erı el nem kezdett dolgozni. Az olajcsepp mérete optikai úton meghatározható, így a következı egyenlıség írható fel:

                            mg = Vρg= QE = Q U/d,

ahol m az olajcsepp tömege, V a térfogata, ρ a sőrősége, Q a töltése, E a kondenzátor
lemezei közötti térerısség, U a feszültség, d a távolság. Az U feszültség és a lemezek d
távolsága mérhetıek, így megkapjuk az olajcsepp töltését.
Millikan azt tapasztalta, hogy minden esetben az eleminek tekinthetı töltés egész számú
többszörösét kapta, vagyis az elemi töltés a legkisebb töltésegység: Q = n 1,6· 10-19 C.

A hidegemisszió
Vigyünk fémtárgyra töltést, és mint azt elektrosztatikából már tudjuk, az azonos töltések taszítása következtében a fém felületén helyezkedik el. Nagyon nagy töltés esetében akkora lehet a taszítás, hogy a töltés egy részét kinyomja a felületbıl. A gázmolekulák zavaró hatását kiküszöbölhetjük, ha légritkított térben végezzük a kísérletet. A jelenség neve hidegemisszió.

A Richardson-hatás
Richardson angol fizikus figyelte meg azt a jelenséget, hogy minden külsı hatás nélkül
is kilépnek negatív töltések a fémekbıl.
Légritkított tértbe helyezzünk egymással szembe két elektródát. Az egyiket földeljük le,
a másikra gyenge pozitív feszültséget adjunk. Azt tapasztaljuk, hogy az elektródák között
áram indul meg. A töltés a leföldelt töltéshordozóból a hımozgás hatására kiléphet a
felületbıl, és engedve a gyenge vonzásnak átvándorol a másik elektródára.

Az izzóelektromos hatás
Magas hımérsékleten erısen megnı a Richardson-hatás, az izzó fémbıl már tömegesen
távozik a negatív töltés. Ez az izzóelektromos hatás, vagy termikus emisszió.
Ez utóbbi két jelenség az alapja a katódsugárcsı, így például a tv-képcsı mőködésének.
Ezekben a katódot általában külön áramkör főti és hevíti izzásig.

A katódsugárcső
Helyezzünk légritkított térbe két elektródát, s kapcsoljunk rá feszültséget. Nagyon kis
gáznyomás esetén a katód egy láthatatlan sugárzást bocsát ki, amely abból vehetı észre, hogy a katóddal szemben, ahol a sugárzás az üvegburát éri, fényjelenség jön létre, amennyiben az üveg belsı felületét fluoreszcens anyaggal vonják be. Ez a sugárzás a katódsugárzás. A katódsugárzást J.J.Thomson vizsgálata elıször. 1897-ben végzett kísérleteiben elektromos és mágneses terek segítségével a katódsugárzásban megjelenı részecske eltérülését vizsgálta, s ennek segítségével meghatározta annak fajlagos töltését. Az elemi részecske töltése ismeretében kiszámítható volt annak tömege is, ezért ezt az idıpontot tekintjük az elektron felfedezésének.
A katódsugárcsıben izzókatódot alkalmazunk, a katód és az anód közé ismert
gyorsítófeszültséget kapcsolunk. Az anód nyílásán keskeny nyalábban áthaladó, közel
egyforma sebességő elektronok ismert erısségő homogén mágneses térben ugyanazon a
körpályán mozognak, amelynek sugara meghatározható.
A körmozgásra vonatkozóan a centripetális erıt a mágneses Lorentz-erı szolgáltatja:
mv2/R = qvB, innen v = qRB/m, ahol m az elektron tömege, v a sebessége, q a töltése, R
a körpálya sugara, B a mágneses indukció. A gyorsítási munka megadja az elektron mozgási energiáját: qU = mv2/2.
A két egyenletet összegezve:





Az elemi töltés ismeretében az elektron tömege: m = 9,1 · 10*-31 kg.

   Tapasztalati tény, hogy a testek minden hımérsékleten hıt sugároznak ki
elektromágneses hullámok formájában. Ez a hımérsékleti sugárzás. Ez a sugárzás a
hımérséklet növekedésével nı.
Kirchoff sugárzási törvénye szerint anyagi minıségtıl függetlenül minden anyagra
igaz, hogy a kibocsátás és az elnyelés intenzitásának hányadosa egy adott frekvencia- és
hımérsékletérték mellett állandó. Abszolút fekete test az az ideális test, amely minden érkezı sugárzást teljes egészében elnyel.
 A Stefan-Boltzmann-törvény szerint az egységnyi felületrıl egységnyi idı alatt
kisugárzott energia arányos a test abszolút hımérsékletének negyedik hatványával.
A Wien-féle eltolódási törvény szerint minden hımérséklethez tartozik egy
hullámhossz, ahol a sugárzás intenzitása maximális.
 Ez a hullámhossz fordítva arányos a hımérséklettel.
Max Planck ezekre a törvényszerőségekre próbált magyarázatot adni, és arra a
következtetésre jutott, hogy egy test részecskéi (atomok, molekulák, vagy ionok) nem
folytonosan, hanem adagokban (kvantumokban) sugároznak ki és nyelnek el energiát. Ez a
véges energiaadag arányos a sugárzás frekvenciájával.
E = hf,   Az arányossági tényezı a h = 6,6 · 10*-34 Js, amelyet ma Planck-állandó néven ismerünk.

A kristályok fajhıje
Dulong és Petit mérései a legtöbb kristály molhıjét – magas hımérsékleten – 25 J/K
értékőnek mutatták. A kristályok többségénél széles hımérsékletnél jó közelítés a Dulong-
Petit-szabály. Alacsony hımérsékleten azonban molhı értéke erısen csökken.
A válasz sokáig váratott magára, végül Einstein oldotta meg a kérdést 1906-ban.
A kristály nem képes akármilyen kis energiát felvenni, hanem csak egy meghatározott
kis energiaadag egész számú többszörösét. Ez az energiakvantum arányos a frekvenciával, az arányossági tényezı a Planck-állandó. Einstein feltételezte, hogy a kristályban minden
rugalmas hullám azonos frekvenciájú, ami nem helyt álló, így késıbb Peter Deybe
helyesbítette.
A jelenség ezen magyarázata szintén az energiakvantum létezését támasztotta alá.