kép, ha a leképező eszközt elhagyó sugárnyaláb széttartó, a képet a sugarak
meghosszabbításában látjuk.
Gömbfelülető lencsék és tükrök esetén nem tökéletesen valósul meg az optikai
leképezés, de kis nyílásszögő tükrök, ill. vékony lencsék esetén nagyon kicsi a leképezés
hibája.
Sík tükör
Sík tükrök esetén a látszólagos kép megegyezik az eredetivel, és azonos távolságban
látszik.
Homorú tükör
Optikai padra helyezzünk homorú tükröt, egy égő gyertyát és egy ernyőt. A gyertya
tologatásával keressük meg a gyertya lángjának éles képét az ernyn. ( ábra a,)
A következő nevezetes szerkesztővonalakat használhatjuk (ábra b,):
- a fókuszon átmenő sugarat, amely visszaverıdés után párhuzamos az optikai
tengellyel;
- az optikai tengellyel párhuzamos sugarat, amely visszaverıdés után átmegy a
fókuszon;
- a geometriai középponton átmenı sugarat, amely önmagába verıdik vissza;
- a tükör középpontjába irányított sugarat, amely az optikai tengellyel szimmetrikusan
verıdik vissza.
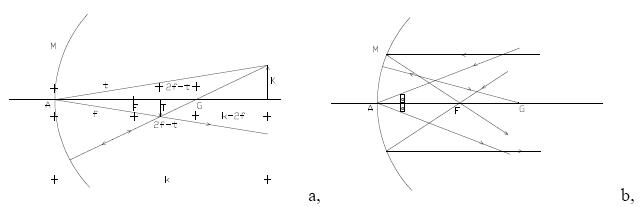
Az ábrán látható (felső ábra) két hasonló háromszög: K : T = k : t, illetve
K : T = (k – 2f) : ( 2f – t).
A kettőt egybevetve kapjuk a leképezési törvényt:

Teljesen hasonló módon lehet domború tükörre is levezetni a leképezési törvényt.
Nagyításnak nevezzük az előjelesen vett képtávolság és tárgytávolság arányát.
N = k / t = f / t - f.
Negatív a nagyítás értéke, ha 0 < t < f.
Ha f < t < 2f , akkor a kép nagyított és fordított állású, ill. valódi.
Ha 2f < t, akkor a keletkező kép kicsinyített, fordított állású, valódi
Ha f = t, akkor nem keletkezik kép, a fókuszból induló sugarak a tükörrıl visszaverődve
párhuzamosan haladnak.
Optikai padra helyezünk egy domború lencsét, egy égı gyertyát, és egy ernyőt. A
gyertya tologatásával keressük meg a gyertya lángjának éles képét az ernyőn.
A következő nevezetes szerkesztéseket hajthatjuk végre ( ábra):
- a fókuszon átmenı sugarat, amely törés után párhuzamos az optikai tengellyel;
- az optikai tengellyel párhuzamos sugarat, amely törés után átmegy a fókuszon;
- a lencse középpontjába irányított sugarat, amely törés nélkül halad tovább.

Az ábrán látható két hasonló háromszögre felírhatjuk, hogy:
K : T = k : t, illetve K : T = (k – f) : f.
A kettőt egybevetve a leképezési törvényt kapjuk:

A homorú tükör lépalkotásával teljesen analóg módon vezethetjük be a nagyítást.
N = k / t = f / t – f.
- Negatív a nagyítás értéke, ha 0 < t < f, ekkor a kép egyenes állású, nagyított.
- Ha f < t < 2f, akkor a keletkezı kép nagyított fordított állású, valódi.
- Ha 2f < t, akkor a keletkező kép kicsinyített, fordított állású, valódi.




