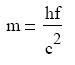Tapasztalati tényként ismert az a jelenség, hogy fény hatására a fémek felületérıl
elektronok lépnek ki. Ez a fotoeffektus, azaz a fényelektromos jelenség.
Az elektronok kilökıdése a fém felületérıl csak a fény frekvenciájától függ,
intenzitásától nem. A vörös fény nem, az ultraibolya fény a legtöbb fém esetében elegendı a kilökıdéshez. A fény intenzitása, csak a kilépı elektronok számát határozza meg, a kilépés bekövetkezését, és a kilépı elektron energiáját nem. A problémát Einstein oldotta meg, felhasználva a fény, mint elektromágneses hullám adottságát.
A fény nem folytonosan, hanem adagokban, kvantumokban szállítja az energiát. Egy
energiakvantum nagysága arányos a fény frekvenciájával. E = hf.
Az elektromágneses hullámban terjedı energiakvantum a foton. Az anyagban kötött
elektron egyszerre mindig csak egy fotonnal találkozik, amelynek energiája nagyobb kell
legyen az elektron kötési energiájánál ahhoz, hogy az elektron kiszabaduljon. Ezzel a
gondolattal lehetıvé válik a kötési energia mérése is.
Erısen légritkított üvegedényben helyezzünk el fémlapot, majd vele szemben egy másik
elektródát. A két elektródát összekötve és a fémlapot megvilágítva, a körben áram folyik.
Kapcsoljunk a két elektródára olyan feszültséget, hogy a fémlap legyen pozitív töltéső, és
változtassuk úgy a feszültség nagyságát, hogy a kezdeti elektronáramlás az ellentér hatására éppen megszőnjön.
Az így mérhetı feszültséget megszorozva az elektron töltésével, megkapjuk azt a munkát, amit a tér végzett, miközben a fémlapból valamilyen sebességgel kilépı elektront lelassította.
Ez tehát éppen egyenlı az elektron kezdeti mozgási energiájával.
A foton energiájának egy része tehát a kilépési munkát szolgáltatta, másik része pedig az
eltávozó elektron mozgási energiáját adta. A következı összefüggés írható fel:
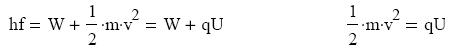
Ismerve a fény frekvenciáját a kilépési munka innen számítható. A jelenség gyakorlati
alkalmazására a fotocellák a legjobb példák, melyek ezen elv alapján mőködnek.
A Compton-effektus
Compton amerikai fizikus végezte el azt a kísérletsorozatot, amelyben nagy energiájú
elektromágneses fotonok szóródását figyelte meg lényegében szabad elektronokon. Ennek
során az elektromágneses hullám kvantuma, a foton úgy viselkedett, mint egy részecske, azaz a megszokott energia- és impulzus-megmaradási tételek igaznak bizonyultak, ha a foton impulzusát a következıképpen határozzuk meg.
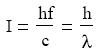
ahol c az elektromágnese hullám sebessége, λ pedig a hullámhossza. A foton tömege így
a következı: