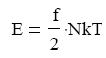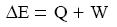Physical blog

   A szilárd, folyékony és gáz halmazállapotú anyagok molekulákból épülnek fel. Ezek a
molekulák között ún. intermolekuláris erő hat. Ez az erı fıként elektromos jellegő, és ha a
részecskéket túl közel akarjuk vinni egymáshoz a vonzás taszításba vált át. Ez az egyik oka,
amiért a folyadékokat nem tudjuk összenyomni. Az egyensúlyban lévı molekulának van
potenciális (helyzeti ), és kinetikus energiája. A kinetikus energia a hımérséklet emelésével
növekszik, elég magas hımérsékleten, pedig túllépheti a potenciális energiát. Ez a pont a
forráspont. Ha a hımérsékletet csökkentjük, akkor a kinetikus energiája alacsonyabb lesz,
megváltozik a molekula viselkedése. A folyadék megfagy.

Az ideális gázok kinetikus modellje: A molekulák mérete elhanyagolható a közöttük lévı
üres térrészhez képest. A részecskék egymással is és az edény falával is tökéletesen
rugalmasan ütköznek, az egyes ütközések között pedig egyenes vonalú egyenletes mozgással haladnak. A gázmolekulák rendezetlenül haladnak, és csak az ütközések pillanatában van közöttük kölcsönhatás.

Ezeket a feltételeket alkalmazva egy adott állapotban lévı gáz fontos fizikai jellemzıi
kifejezhetık a molekulák adataival.

Határozzuk meg a gáz nyomását egy adott tartáj falára, mint a molekulák
időegységkénti lendületváltozását egységnyi falfelületen.





de ha ki akarjuk terjeszteni a képletünket a tér mindhárom irányába, nemcsak x irányba,
akkor

  Az ideális gázok nyomására két fontos kifejezést ismerünk:






Ha két kifejezést integráljuk:





ε a gázmolekulák átlagos kinetikus energiája. Látható, hogy ez az energia a gáz abszolút
hımérsékletével arányos.





A gáz teljes belső energiája a molekulák kinetikus energiájának összege, amely
egyatomos ideális gázra kizárólag a haladó mozgásból származó kinetikus energiát jelenti:




Határozzuk meg, hogyan függ a gázmolekulák átlagos sebessége a hımérséklettıl, ill. a
nyomástól:

   Az egyatomos gázok atomjai rendezetlen mozgásuk során csak haladó mozgást
végeznek, a kétatomos gázmolekulák viszont a haladó mozgáson kívül forognak is, mégpedig a két fő szimmetria tengely körül. Ezért hordoznak a kétatomos molekulák több energiát, mint az egyatomos gázok részecskéi. Ez az f-el jelölt szám a szabadsági fokok száma, amely tehát egyatomos gázokra f = 3, kétatomos gázokra f = 5, többatomos gázokra f = 6, mivel a kettőnél több atomos molekulák forgása 3 tengely körüli. Tehát a gázok belső energiája általánosan a következő alakban adható meg:





Az ekvipartíció tétele szerint, amely az energia egyenletes eloszlásának törvénye, a
gázmolekula minden egyes szabadsági fokára, ½ kT átlagos kinetikus energia jut.

A molekulák hőmozgását legegyszerőbben melegítéssel, hıközléssel növelhetjük. A
hőközlés mértékét, a hőmennyiséget a fizikában Q-val jelöljük. Ezen kívül a belső energiát, mechanikus munkavégzéssel is változtathatjuk ( W ). Ezen megfontolásokat figyelembe véve:

A termodinamika elsı főtétele szerint egy anyagi rendszer belső energiájának
megváltozása egyenlő a közölt hő és a rendszeren végzett mechanikai munka előjeles
összegével.



A tétel azt fejezi ki, hogy egy rendszeren belül semmiféle energia nem keletkezhet, vagy
tőnhet el. Tulajdonképpen ez a tétel zárja ki az ún. elsőfajú örökmozgó létezésének
lehetőségét, amely úgy adna le környezetének energiát, hogy közben a saját belső energiája nem csökkenne.

   Kiindulva a termodinamika elsı fıtételébıl, vizsgáljunk meg egy zárt tartályban lévı
ideális gáz melegítését. Állandó térfogat miatt nincs mechanikai munkavégzés, így:




Mivel egy adott mennyiségő ideális gázra a 3R/2M tényezı a tömegtıl és a
hımérséklet-változástól függetlenül állandó, ezért az állandó térfogaton felvett hı a
következı:



ahol az anyagra jellemző:





állandó, a fajlagos hőkapacitás.




A munkavégzés negatív, hiszen a táguló gáz a környezetén végez munkát a külsı,
állandó nyomás ellen: W = -p    V. Mindezek alapján a szükséges hı, amit a rendszerbe kell
adni:








Látható, hogy az állandó nyomáson vett:





hıkapacitás értéke nagyobb, mintha
állandó térfogaton melegítenénk. A két speciális állapotváltozáshoz tartozó hıkapacitás
kifejezését összevetve megkapjuk az ún. Robert Mayer-egyenleteket:





A két hıkapacitás arányát a görög κ-val jelöljük, és fajhıhányadosnak nevezzük. A
szabadsági fokok számával kifejezve:




tehát például kétatomos gázokra a fajhıhányados: κ = 7/5.

Adiabatikus egy állapotváltozás, ha a Q = 0. Alkalmazva az elsı fıtételt az adiabatikus
folyamatra azt tapasztaljuk, hogy a belsı energianövekedést csak külsı munkavégzés
okozhatja, illetve a gáz kizárólag a belsı energiájának rovására végezhet tágulási munkát. Az adiabatikus állapotváltozásra a következı összefüggést alkalmazzuk:




ahol κ a már bevezetett fajhıhányados. A P-V diagramon ábrázolva egy adiabatikus
állapotváltozást, a kapott görbe neve adiabata. Mivel a κ értéke minden gázra nagyobb
egynél, az adiabatikus változás egy, az izotermánál meredekebb görbével adható meg.

   Hétköznapi tapasztalatok alapján jól ismert halmazállapot-változás, például a fagyás,
olvadás, párolgás, forrás, lecsapódás, de talán kevésbé ismert fogalom a szublimáció.
Ezek az állapotváltozások az ún. elsőrendű fázisátalakulások. Ez azt jelenti, hogy egy anyagra jellemző hőmérsékleten ugrásszerűen változnak a fizikai jellemzők.
Ezek az anyagra jellemző hőmérsékletek – olvadáspont, fagyáspont, forráspont, stb. – nagyban függnek a külső hatásoktól, elsősorban a nyomástól.
A tapasztalatok szerint a fázisátalakuláshoz szükséges hő mindig az átalakulást szenvedő anyag tömegével arányos. Q = Lm.

Az anyagra jellemző L állandó, a folyamattól függően olvadáshő, párolgáshő, illetve
forráshő néven ismert, és számértéke megadja az egységnyi tömegő anyag halmazállapotának megváltozásához szükséges hőmennyiséget. Minden anyaghoz tartozik egy meghatározott hőmérséklet, amely felett az adott anyag csak gáz halmazállapotú lehet, és bármilyen nagy nyomással sem cseppfolyósítható.
Ez a hőmérséklet az anyag kritikus hőmérséklete. Az éppen kritikus hőmérsékleten lévő gáz lecsapódásához szükséges nyomás a kritikus nyomás.