2.10. A hőfolyamatok iránya, a termodinamika második és harmadik főtétele
2008.01.13. 17:19 :: peiszisz
tehát megfordítható és nem megfordítható folyamatokat. Megfordítható folyamat, ha a
lehőtött vízzel (jéggel) hıt közölve ismét folyékony vizet kapunk, bár ehhez külsı segítséget is adunk. Azonban megfordíthatatlan folyamatnak tekintjük azt, ha a talajra leesı, és közben hőt termelı testet hőtve a test visszarepülne oda, ahonnan leesett.
A termodinamika második fıtétele szerint a természetben külsı behatások nélkül
mindig a hımérséklet kiegyenlítıdésére irányuló folyamatok zajlanak le: azaz a hı magától
nem kerülhet az alacsonyabb hımérséklető helyrıl a magasabb hımérséklető helyre.
A tétel egy másik megfogalmazásában Max Plank szerint nem lehet készíteni és
mőködtetni ún. másodfajú örökmozgót. Ez periodikusan mőködı hıerıgép, amely minden
ciklus végén visszajuttatná a rendszert eredeti állapotába, és közben még hasznosítható
munkát is végezne.
A harmadik megfogalmazáshoz be kell vezetnünk az entrópia fogalmát, amely a
rendezetlenség mértéke. Ezt a mennyiséget a fizikában S-el jelölik és egy rendszer
mozgásállapotára és energia-eloszlására jellemzı értéket mutat.
A termodinamikailag zárt rendszerek entrópiája az ideális, reverzibilis folyamatokban
állandó marad, a valóságos, spontán folyamatokban viszont növekszik. Egy rendszer
entrópiája az egyensúlyi állapotban lesz maximális. Ez az entrópiamaximum elve.
Végül a termodinamika harmadik főtétele azt a tapasztalati tényt rögzíti, hogy az
abszolút zérus hımérséklet, a 0 Kelvint véges sok lépésben egyetlen anyagi rendszer sem
érheti el. Ugyanis az anyagok entrópiája 0 Kelvin közelében nagyon kicsi, tart a nullához,
ezért a hıkapacitás is tart a nullához, ami azt jelenti, hogy egészen kicsi Q hı már végtelen
nagy hımérséklet-változást eredményezne. Az abszolút zérus pont tehát nem érhetı el. Ez a Nenst-tétel.
Szólj hozzá!
3.1.1. Alapjelenségek
2008.01.13. 17:16 :: peiszisz
papírdarabokat magához vonzz, viszont ha egy másik megdörzsölt mőanyag vonalzót
közelítünk hozzá, taszítani fogja azt. Általánosan is igaz, hogy dörzsölés hatására kétféle
elektromos állapot jön létre, és ez az állapot attól is függ. hogy mivel dörzsöljük az illetı
anyagot.
Az elektromos állapotban lévı test elektromosan töltött, illetve a testnek elektromos
töltése van. Az azonos töltéső anyagok taszítják, míg az ellentétes töltéső anyagok vonzzák egymást. A bırrel dörzsölt üvegrúd töltését pozitívnak, a posztóval dörzsölt ebonitrúdét negatívnak nevezzük. Dörzsöléskor csak szétválasztjuk a töltéseket.
Töltés a semmibıl nem keletkezik, és nem is tőnhet el. Zárt rendszer töltése állandó.
Vezetık és szigetelők
Próbáljunk egy kezünkben tartott fémrudat dörzsöléssel feltölteni, azaz elektromos
állapotba hozni. Ez csak akkor sikerül, ha a fémrudat egy mőanyag vagy üvegnyélhez
erısítjük és így dörzsöljük. Ekkor a fémrúd az egész felületén töltött lesz, de ezt a töltést
azonnal el is veszíti, ha valamelyik pontjában hozzáérünk az ujjunkkal. Ezzel szemben nem
veszíti el töltését egy feltöltött plexirúd, ha egy ponton megérintjük. Joggal feltételezhetjük, hogy a töltések a fémekben igen mozgékonyak, de pl. a plexirúdban már nem. Az elektromos állapotot a fémek nagyon jól tudják közvetíteni, azaz jó vezetők. A plexirúd pedig jól szigetel, azaz rossz vezető. Ennek megfelelıen a vezetés és a szigetelés nem határolható el élesen egymástól. Jó vezetıknek tekintjük a fémek, az emberi test, a grafit, a föld, az elektrolitok, stb. Jó szigetelı, azaz rossz vezetı pl. a plexi, az üveg, a porcelán, a desztillált víz, stb.
Coulomb törvénye
Coulomb törvénye szerint két pontszerő töltés között ható erı egyenesen arányos a két
töltés szorzatával, és fordítottan arányos a köztük lévı távolság négyzetével, azaz
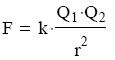
A törvény felállításához nem kellett a töltéseket mérıszámokkal jellemezni. A törvény
lehetıséget ad a töltés egységének definiálására. Gyakorlati szempontok miatt ( SI rendszer ) azonban a töltés egységét a Coulomb törvénytıl függetlenül választották meg. Ezt a töltésegységet Coulomb-nak nevezzük, jele: C. A k arányossági tényezı értéke közelítıleg:
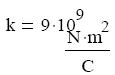
Eszerint 1 C töltése annak a pontszerő testnek van, amely egy másik , ugyanakkora
töltéső pontszerő testet 1 méter távolságból 9 ×10^9 × N erıővel taszít. A valóságban ekkora töltést kis- mérető testeknek nem adhatunk, csak a töredékét.
Ha egy ponttöltésre egyszerre több erı hat, akkor a tapasztalat szerint érvényes a
szuperpozíció elve, azaz a Coulomb törvény segítségével kiszámított erık vektori összege
adja meg az adott ponttöltésre ható eredı erıt.
Szólj hozzá!
3.1.2. Az elektromos tér és térerősség
2008.01.13. 17:10 :: peiszisz
Faraday alapgondolata szerint a töltések nem közvetlenül hatnak egymásra, hanem két
elektromosan töltött test között a térben van valami, ami a hatást közvetíti.
Ezt a gondolatot úgy fogalmazzuk meg, hogy az elektromos állapotban lévő test maga körül ún. elektromos mezőt, vagy más szóval erőteret kelt, és ez az erő hat a testtől távol eső más testre. Az olyan elektromos mezőket, amelyeket nyugvó töltések keltenek, vagyis amelyek időben állandóak, elektrosztatikus mezőknek nevezzük.
Ha két vagy több töltés hoz létre egy közös mezőt, az együttes mezőnek bármely testre
kifejtett erőhatása mindenütt a vektori összege azoknak az erőknek, amelyet az egyes töltések külön-külön, egyedül hoznának létre. Ez az elv az elektromos mezők szuperpozíciójának elve.
Az elektromos mező bármely pontjába helyezett testre ható elektromos erő egyenesen
arányos az odahelyezett test töltésével. A térerősség tehát megegyezik a testre ható erőés a test töltésének hányadosával.
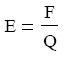
Ha figyelembe vesszük Coulomb törvényét, akkor a pontszerő töltés körül kialakuló
elektromos mező térerőssége egyenesen arányos a mezőt keltő töltéssel, és fordítottan arányos a tőle mért távolság négyzetével
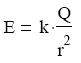
Az elektromos tér szemléltetése erővonalakkal
Az erővonalak olyan elképzelt görbék, amelyek a pozitív töltésből indulnak és a negatív
töltésen keresztül végződnek, és az erővonal érintője minden pontban a térerősségvektor.
Minden ponton csak erővonal halad át, hiszen ha kereszteznék egymást, akkor nem lenne
egyértelmű a térerősségvektor iránya.
Egységnyi felületen áthaladó erővonalak száma az ún. fluxus, jele:ψ, egysége: Nm²/C.
Amennyiben a felület nem egységnyi, akkor A. Tehát a fluxus: ψ = EA.
Az elektromos fluxus természetesen nem csak homogén felületen, hanem inhomogén
felület esetén is számolható. Ekkor az az eljárás, hogy az adott felületet részekre bontva
számoljuk, majd összeadjuk őket. Amennyiben a felület egy gömb, mint például egy
pontszerő töltés erőtere, akkor a képletünk a következő formára alakul:
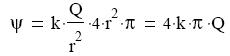
Zárt felületre az elektromos fluxus egyenlő a bezárt össztöltés 4kπ-szeresével, hiszen a
tőltés erőtere gömb felületet hoz létre. Ez a Gauss-tétel, avagy Maxwell első törvénye.
Munkavégzés elektromos térben, a feszültség
Az elektromos tér F = QE erőt fejt ki a benne lévő Q töltéső testre, ezért a test
mozgatásakor általában munkát is végzünk. W = F · s = EQs · cos(alfa).
Amennyiben cos(alfa)= 1,vagyis ha a munkavégzés térerősség irányú, akkor kimondhatjuk,
hogy ha egy Q töltést A-ból B pontba viszünk W munkával, akkor a W/Q állandót az A, B
pontra vonatkozó feszültségnek nevezzük, és U-val jelölük.
A feszültség jele a Volt (V). U =W/Q.
Ha a munkavégzés egy Q töltésen zárt térben történik, például egy magába visszazáródó
görbe mentén (kör), akkor az összes végzett munka zérus, azaz zárt hurokra a körfeszültség nulla. Ez az elektrosztatika II. törvénye, avagy Maxwell II. törvénye.
Potenciál
Az eddigi megállapításainkból tehát kimondhatjuk, hogy egy Q töltésen akkor végzünk
munkát, ha az elmozdulás-vektor a térerő-vektor irányába mutat. Ha az elmozdulás-vektor
merőleges a térerő-vektor irányára, akkor nincs fizikai értelembe vett munkavégzés.
Válasszunk ki egy nullaszintet (A), majd ehhez képest adjuk meg azt a munkát, amelyet
végeznünk kell a tér ellenében ahhoz, hogy a töltést (B) felületre juttassuk. Ekkor azt
mondhatjuk, hogy a Q töltés helyzeti energiája a (B) ponton W, így a W/Q hányados, az erre a szintre jellemző érték, neve a potenciál, jele:U. U = W/Q = kQ/r.
A potenciál tulajdonságából fakad, hogy két pont között a potenciálkülönbség, azaz két
pont potenciáljának különbsége:
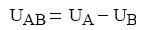
Szólj hozzá! · 1 trackback
3.1.3. Kapacitás, Kondenzátorok
2008.01.13. 17:00 :: peiszisz
Egy r sugarú vezetıgömb kapacitását könnyen meghatározhatjuk: C = Q/U = Q/kQ/r =
r/k.
Kondenzátor (sűrítő): Olyan berendezés, melynek célja, hogy minél kisebb térrészben
minél több töltést tároljon, minél kisebb feszültségen, vagyis minél nagyobb legyen a
kapacitása.
Síkkondenzátorok: Két nagy felülető, egymással párhuzamos, egymáshoz közel
helyezett sík fémlemez.
A síkkondenzátor lényegében két azonos kiterjedésű párhuzamos fémlemez, amelyeket
+Q és –Q töltéssel látunk el. A két lemez három tartományra bontja a teret. Az egyes
lemezektől származó térerősségek a két szélső tartományban ellentétes irányúak, ezért ott az összegük nulla, a középső tartományban pedig azonos irányúak, így az összegük:
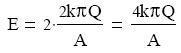
Ha a lemezek távolsága d, akkor a feszültség:
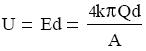
így a kapacitás
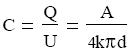
A síkkondenzátorok kapacitása tehát egyenesen arányos a felülettel, és fordítottan
arányos a lemezek távolságával.
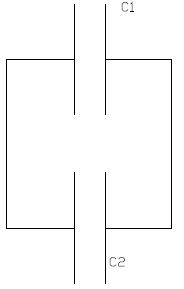
Kondenzátorok kapcsolása: Soros kapcsolás.
.jpg)
Kapcsoljunk össze két kondenzátort úgy, hogy fémesen összekötjük egy-egy lemezüket,
más néven fegyverzetüket. (ábra). Az így kapott közös pont, a B pont. Ha +Q töltést
adunk az A felőli lemeznek, és a C pontot leföldeljük, akkor a két kondenzátor a megosztás
révén azonos töltésre töltődik. A feszültség A és C között a két kondenzátor feszültségének összege, azaz U = U(alsó index:AC) = U(alsó indexAB) + U(alsó indexBC).
A kondenzátorrendszer Q töltést tárol. A rendszer helyettesíthető olyan C kapacitású
kondenzátorral, amelyen Q töltés szintén U feszültséget hoz létre. Felhasználva, hogy U =
Q/C, a feszültségre az alábbi összefüggés írható fel.
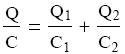
A kifejezést Q-val egyszerősítve megkapjuk a soros kapcsolású
kondenzátorok eredı kapacitására vonatkozó összefüggést:
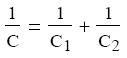
Sorosan kapcsolt kondenzátorok esetén az eredő kapacitás reciproka az egyes
kapacitások reciprokainak összege.
Párhuzamos kapcsolás: Kapcsoljunk össze két kondenzátort úgy, hogy fegyverzeteiket
páronként összekötjük, és vigyünk fel a rendszerre Q töltést . A helyettesítő kondenzátor C kapacitása a következőképpen határozható meg. A kondenzátorok feszültsége azonos kell hogy legyen, úgy, hogy a helyettesítő kondenzátor töltés egyenlő a párhuzamosan
kapcsolt kondenzátorokon tárolt töltések összegével.
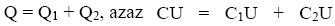
A közös feszültséggel osztva, a párhuzamosan kapcsolt
kondenzátorok eredő kapacitását kapjuk:
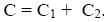
A párhuzamosan kapcsolt kondenzátorok kapacitásai összeadódnak.
A kondenzátor energiája: Legyen egy adott pillanatban a lemezek közti fezsültség U,
és egy (delta)Q töltést vigyünk át a kondenzátor egyik fegyverzetérıl a másikra a már kialakult elektrosztatikus tér ellenében. Ekkor a töltés átviteléhez szükséges munka:
(delta) W = U ·(delta)Q.
Az U feszültség eléréséhez szükséges összes munka, pedig
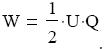
A képlet a kondenzátor kapacitásának felhasználásával átírható.
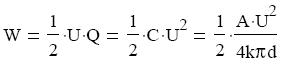
Ezt a térerősséggel kifejezve:
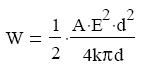
Ha egyszerősítünk d-vel és elosztjuk az oldalakat a kondenzátor térfogatával,
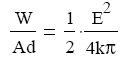
amit tovább egyszerősítünk két új fogalom bevezetésével. Az ω = W/Ad mennyiség az
egységnyi térfogatban található energia, azaz az elektrosztatikus tér energiasőrősége. Az
1/4πk = ε(alsó index:0) azaz a vákuum dielektromos állandó behelyettesítésével:
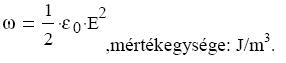
Kondenzátor szigetelőkkel: Töltsünk fel egy kondenzátort Q töltéssel, majd tegyünk
lemezei közé egy szigetelő üveglapot. Azt tapasztaljuk, hogy a feszültség csökken. Ha az
üveglapot eltávolítjuk, akkor a feszültség az eredeti értékére áll vissza, azaz a kondenzátor töltése nem változott meg. A jelenséget azzal magyarázhatjuk, hogy a szigetelıanyag behelyezésével megváltozik a kondenzátor kapacitása. Mivel a feszültség változatlan töltés mellett csökkent, a kapacitás megnőtt. Megállapodás szerint az
ε(alsó index:r) = C/C(alsó index:0) hányados értékét, ami csak a behelyezett szigetelőanyagra jellemző, az anyag relatív permittivitásának
nevezzük. Számértéke megmutatja, hogy hányszorosára nő a kondenzátor kapacitása az üres kondenzátoréhoz képes.
1 komment
3.1.4. Az elektromos áram fogalma, az áramerősség
2008.01.13. 16:38 :: peiszisz
feltöltött fémlemezt. Függesszünk közéjük cérnaszálon egy kisméretű fémtárgyat vagy
grafitporral bevont pingponglabdát.
Azt tapasztaljuk, hogy a labda lengésbe jön, és a két lemez érintése során töltéseket szállít át a nagyobb potenciálú lemezrıl a nulla potenciálú lemezre. A töltésszállítás mindaddig tart, míg elegendő nagy a potenciálkülönbség.
Az ilyen töltésáramlást konvekciós áramnak nevezzük, ami azt jelenti, hogy a töltések
mozgása anyagárammal jár együtt.
Az elektromos töltések adott helyen való áthaladása az elektromos áram. Az áram
intenzitását az áramerősség jellemzi, amely megmutatja, hogy mennyi töltés halad át az adott helyen egységnyi idő alatt. Jele: I, nagysága: I = (delta) Q/ (delta)t, ahol Q jelenti a vezető teljes keresztmetszetén t idő alatt átáramló töltés mennyiségét.
Az elektromos áramerősség mértékegysége az amper, jele: A. Az 1 A erısségő áram
esetén a vezető minden keresztmetszetén 1 s alatt 1 C töltés halad át.
Egyenáram ( stacionárius áram ) esetén az I = (delta)Q/ (delta)t hányados állandó értéked ad, függetlenül a (delta)t nagyságától.
Abban az esetben, ha ez a hányados nem állandó, akkor értéke az adott időtartamra
vonatkozó átlagos áramerősséget adja meg. Az áram iránya megállapodás szerint a pozitív
töltések mozgási iránya. Ez azt jelenti, hogy az áram iránya a fémekben ellentétes irányú az elektronok tényleges mozgási irányával.