Physical blog

  A munka fogalma: A fizikában egy erı munkája az erı és az erı irányába történı
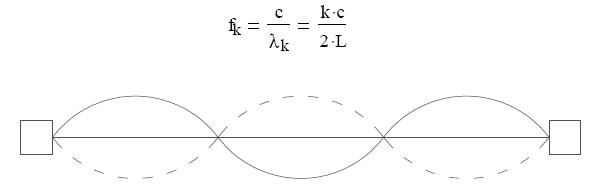
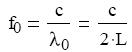elmozdulás szorzata. Munkavégzésünk nagysága attól függ, hogy mekkora erıvel és milyen
hosszú úton mozgatunk egy testet. Abban az esetben, ha az erı és a test elmozdulása
egyirányú, a munkán az F erő és s elmozdulás szorzatát értjük: W = F · s, ahol w a munka
jele, mértékegysége: ( kg · m²/s² = 1 J = egy Joule). Abban az esetben, ha az erı és az
elmozdulás nem egyirányú, az erıt felbontjuk elmozdulás irányú, és arra merıleges
komponensekre. A merıleges komponens munkája nulla, így általánosítva kimondhatjuk,
hogy az elmozdulásra merıleges erı nem végez munkát. Ha az erı és elmozdulás-vektor
által bezárt szög α, akkor a képletünk: W = F · s · cosα. Mivel cos90 = 0, a merıleges
komponens is nula.

Ha egy tömegpontra több erı hat, akkor az eredı erı munkája egyenlı az egyes erık
munkáinak algebrai összegével:




Speciális munkavégzések

Emelési munka: Emeljünk fel egy testet egyenletesen. Ebbıl következik, hogy a testre
ható erık eredıje nulla, tehát F = m · g. Az F erı munkája kiszámítható:



A nehézségi erı munkájánál az m·g erı iránya ellentétes az elmozdulással:



Ha a testet lefelé engedjük, az elıjelek a két munka között felcserélıdnek.

Súrlódási munka: Vízszintes talajon gyakran mozognak testek állandó erı hatására
állandó sebességgel. Ilyenkor a húzóerı a súrlódási erı ellenében végez munkát. Állandó
sebesség esetén a testre ható erık eredıje nulla:



Tehát az F húzóerő munkája:



A súrlódási erı munkája pedig:




A gyorsítási munka: A dinamika alaptörvénye szerint: F = ma, további kinetikai
összegfüggésekből számítva a gyorsítási munka:




Érdekes megfigyelni, hogy a munkavégzés kizárólag a test adataitól függ. Sem az út
sem a húzóerı nem szerepel a végsı megoldásban.

Rugó megnyújtása során végzett munka: Nyújtatlan helyzetbıl kiindulva, növeljük
meg egy D rugóállandójú rugó hosszát x-el. Mivel F= D · x, ezért a következı összefüggést
kapjuk:






A teljesítmény: A munkavégzés szempontjából fontos, hogy az mennyi idı alatt megy
végbe. A munkavégzés gyorsaságát a teljesítmény méri, jele: P. Valamely erı munkájának
átlagos teljesítménye az erı munkájának és munkavégzés idejének hányadosa:




Mértékegysége: J/s = 1 Watt ( W ).

Mivel a munkavégzés nem feltétlenül állandó, ezért definiálnunk kell pillanatnyi
teljesítményt is. A pillanatnyi teljesítmény az adott idıpont környezetében nagyon rövid     t időre számított átlagteljesítménye: P = (delta)W /(delta) t.

Mivel W = F · s, így a teljesítmény P = F ·(delta)s / (delta)t. A pillanatnyi sebesség definíciójából tudjuk, hogy ( v = (delta)s /(delta)t). Tehát: P = F · v.

Az energia: Az energia, mint munkavégzı képesség definiálható. Az energia eltárolt
munka, amely megfelelı körülmények között ismét felszabadul. Az energia a test egy adott
állapotát jellemzi, míg a munka két állapot közötti folyamatot ír le.

A mozgási energia: A dinamika alaptörvényét és a munka definíciójából kiindulva ezt
az egyenletrendszert kapjuk:





A végeredmény csak a test mozgásállapotától függı mennyiségeket tartalmaz, vagyis:


mennyiség a test mozgási energiája, mértékegysége: 1 J – Joule.


A helyzeti energia: Az olyan erıket, amelyek munkája független az útvonaltól,
konzervatív erıknek hívjuk. ( gravitáció- elektrosztatikus erı). Ha egy testet A-ból B pontba visszük, munkavégzésünk, csak a pontok elhelyezkedéseitıl függ.Tehát a test állapotát jellemezhetjük azzal a munkával, amit akkor végzünk, ha a testet egy önkényesen megválasztott pontból ( referenciapont) a tér egy tetszıleges pontjába visszük. A konzervatív erıtér egy pontjában a test potenciális ( helyzeti ) energiája egyenlı azzal a munkával, amivel a testet a referenciapontból az adott pontba juttatjuk. Tehát ha egy m tömegő testet h magasságba juttatok, az elvégzett munka: W = F · s = F · h = m · g · h. Vízszintes elmozdulás esetén a munkavégzés nulla, hiszen az F erı és az elmozdulás
egymásra merőlegesek.

A test mozgása során, ha csökken a potenciális energiája nı a mozgási energiája, és
fordítva. Tehát:




A hatásfoka: A munkavégzés hatásfoka a hasznos és az összes befektetett munka
hányadosa:



mértékegység nélküli mennyiség.

A rezgımozgást végzı testnek a nyugalmi helyzettıl mért maximális kitérése a
rezgőmozgás amplitúdója, jele: A.

Az az idı, amelynek elteltével a rezgı test kitérése és sebessége újra a kezdeti értékkel
egyezik meg, a rezgésidő, jele: T.

Az egy másodpercre jutó rezgések száma, pedig a frekvencia, jele: f. A rezgésidı és a
frekvencia között fordított arányosság áll fenn: T = 1/f.

A rezgőmozgás kitérés-idő függvénye, kapcsolata a körmozgással: Egy körpályán
mozgó test rezgımozgást végez, ahol a test sebességét, a szögelfordulással írjuk le.
α = ωt. Mivel rezgımozgást is végez a test, így kitérése is van.









Harmonikus rezgımozgásról beszélünk, ha a kitérés az idı szinuszos függvénye.

Az α=ωt, a rezgés fázisa. Ha a t = 0 idıpontban a körmozgást végzı testhez húzott
sugár nem vízszintes, hanem azzal φ szöget zár be, akkor ez a φ szög lesz a kezdőfázis
vagy fázisállandó. Így a kitérés:



A sebesség-idő függvény: Az (ábra) szerint a körmozgást végző test
sebességének függőleges vetülete megegyezik a rezgımozgást végző test sebességével.



de mivel R = A-val, vagyis a maximális kitéréssel, így:



Az A·ω kifejezést sebességamplitúdónak is nevezzük, ez a rezgımozgást végzı test
legnagyobb sebessége.

A gyorsulás-idő függvény: A körpályán mozgó test gyorsulása



iránya a kör középpontja felé mutat. Ennek a függılegesre esı vetülete lesz a rezgımozgás
gyorsulása, amely mindig a test egyensúlyi helyzete felé mutat.




Vegyük észre, hogy y-t behelyettesítve:



Az A x w² kifejezést gyorsításamplitúdónak is nevezzük, ez a rezgımozgást végzı test
legnagyobb gyorsulása.

Egyirányú rezgések összetétele: Két azonos frekvenciájú és irányú harmonikus
rezgésnek az eredıje is harmonikus rezgés. Az eredı rezgés frekvenciája megegyezik az
összetevık frekvenciájával, de az amplitúdó különbözik. A két rezgést leíró függvény
legyen:




Keressük az eredı rezgést, ami:




Meg kell határoznunk az eredı rezgés amplitúdóját és kezdıfázisát, hiszen ezeket nem
ismerjük. Az eredı rezgés kezdıfázisának tangense pedig:





Az eredı rezgés amplitúdójának meghatározásához a cosinus tételt alkalmazzuk:




Érdekes görbét kapunk, ha a két rezgés frekvenciája csak kis mértékben különbözik. Az
amplitúdó lassan, a különbségi frekvencia szerint változik, az összetett rezgés kitérésének
burkológörbéit két ellentétes fázisú, kis frekvenciájú harmonikus görbe alkotja. Ez a
jelenség a lebegés.

Egymásra merıleges rezgések összetétele:

A két egymásra merıleges rezgés legyen:

















középponti ellipszis egyenletét kapjuk. Könnyő belátni, hogy tetszıleges φ esetén is
ellipszishez jutunk, csak a tengelyei nem lesznek párhuzamosak az x illetve y tengellyel.
Speciális eset, amikor (w1= w2) és φ = π/2, ekkor ugyanis a két rezgés eredıje
körmozgást eredményez.

Különbözı frekvenciájú egymásra merıleges rezgések eredıjét reprezentáló görbék
analitikus alakját már igen nehéz megadni. Ezek a görbék a Lissajous görbék.

 Már beláttuk, hogy harmonikus rezgımozgás esetén



a gyorsulás arányos a kitéréssel, és mindig az egyensúlyi helyzet felé mutat. Ezt összevetve a dinamika alaptörvényével megállapíthatjuk, hogy egy pontszerő test harmonikus rezgımozgást végez, ha a rá ható erık eredıje a nyugalmi helyzettıl mért távolsággal arányos és mindig a nyugalmi helyzet felé mutat.

Ha egy m tömegő test vízszintes súrlódásmentes felületen, D rugóállandójú rugó hatása
alatt mozog, a rezgésideje:





Láthatjuk, hogy a rezgésidı csak a test tömegétıl és a rugó erısségétıl függ.

Az ingamozgás: Függesszünk vékony fonálra kismérető testet. Ha a test pontszerő és a
fonál tömege elhanyagolható, akkor matematikai ingáról vagy fonálingáról beszélünk.
Abban az esetben, ha a fonálinga kitérése kicsi, a kilengési szög közel megegyezik a szög
szinuszával, így azzal egyszerősíthetünk. Mivel ez a kis kitérés harmonikus rezgımozgást is
végez, megállapíthatjuk, hogy a rendszer rezgésideje:





ahol l a fonál hossza, g pedig a nehézségi gyorsulás.

A súlypontján kívül felfüggesztett, lengeni képes merev test, pedig a fizikai inga. Mivel
ebben az esetben nem pontszerő a testünk, hanem merev testként viselkedik és van
kiterjedése, így a fizikai inga lengésideje:





ahol a Θ a test tehetetlenségi nyomatéka, m a test tömege, s pedig a súlypont és a
felfüggesztési pont távolsága.

A rezgési energia: Rezgımozgást végzı rendszer maximális kitérése esetén (amplitúdó
maximális), ebben a szélsı helyzetben a kitérı test sebessége nulla, itt tehát a teljes energiát a rugalmas energia teszi ki:


ahol D a rugóállandó.

Zérus kitérésnél, tehát a test egyensúlyi helyzeten való áthaladás pillanatában viszont a
rugó nyújtatlan, így az egész energia tisztán mozgási energia:




Ha a sebesség helyébe beírjuk az Aω összefüggésünket, valamint az ω = 2πn értéket,
akkor megkapjuk, hogy:





A csillapított rezgés: Amennyiben a testre a rugóerı kívül más erı is hat, akkor a
rendszer energiája folyamatosan csökken, a rezgés amplitúdója egyre kisebb lesz, a rezgés
csillapodik. Ha a rugóerın kívül csak súrlódási erı hat, a test maximális kitérése minden
félperiódusban ugyanannyival csökken, így az egymást követı amplitúdókra egyenes
fektethetı.(lineáris).

Ha a testet a közegellenállás csillapítja, akkor a test maximális kitérése kezdetben
rohamosan, majd egyre kevésbé csökken, így az egymást követı amplitúdók egy
exponenciális görbére illeszkednek. Ez azért lehetséges, mivel a közegellenállás a sebesség
négyzetével arányosan hat, így az illeszkedıgörbének is négyzetes függvény alakja kell
hogy legyen. Ha csillapítatlan rezgést akarunk létrehozni, akkor gondoskodnunk kell a
súrlódási erık által elvont energia pótlásáról.

Nagy viszkozitású folyadékokban (pl.:méz), megeshet, hogy nem jön létre még egy
teljes rezgés sem. Ezek a rezgımozgások az aperiodikus mozgások.

A kényszerrezgés és rezonancia: Ha egy rezgıképes rendszert egyensúlyi helyzetébıl
kitérítve magára hagyunk, akkor a ún. szabadrezgést végez, amely a környezettıl függıen valamilyen mértékben csillapodik. Ha egy ilyen rendszerre periodikus erı hat, akkor ez az erı gerjeszti a rendszert. Állandó amplitúdójú harmonikus rezgés jön létre, melynek
frekvenciája megegyezik a gerjesztı rezgés vagy erı frekvenciájával, amplitúdója és
kezdıfázisa azonban attól eltér. A gerjesztı erı (külsı periodikus erı) hatására létrejövı
rezgést kényszerrezgésnek hívjuk.

Akasszunk egy laza rugóra egy testet, és a rugó kéznél lévı végét mozgassuk
periodikusan fel-le. Megfigyelhetjük, hogy a frekvencia növelésével a létrejött rezgés
amplitúdója is nı, és egy egészen nagy amplitúdó is kialakulhat. Ha tovább növeljük a
frekvenciát az amplitúdó csökkenni fog.

Az egészen nagy amplitúdó létrejötte a rezonancia. Ekkor a kényszerítı rezgés
frekvenciája közelítıleg megegyezik a rezgıképes rendszer szabad rezgésének a
frekvenciájával, az ún. sajátfrekvenciával.

   Mechanikai hullámnak nevezzük a rugalmas közeg olyan állapotát, amelyben a
rezgési energia térben terjed tova.

Laza rugó egyik végét rögzítsük, a másik végét pedig hirtelen rántsuk meg
hosszirányban. Azt tapasztaljuk, hogy az így létrehozott deformáció végigfut a rugón, majd a rögzített cégérıl visszaverıdik. Ugyanezt tapaszaljuk, ha keresztirányban ráütünk. Ekkor egy ’völgy’ fut végig a rugón. Ha jobban megfeszítjük a rugót, akkor gyorsabban terjed a deformáció, ha kevésbé feszítjük meg, akkor lassabban.

Ha a rugó két végéről egyszerre indítjuk a deformációt, azok mintegy „áthaladnak”
egymáson. A találkozás helyén lévő pontok mind a két deformációnak eleget tesznek, azaz
a két kitérés összeadódik, szuperponálódik. Egy testen két rezgés egyidejű megvalósítását, azaz a két rezgés zavartalan összetételét szuperpozíciónak nevezzük.

Az a legkisebb távolság, amely után (az adott idıpillanatban) újra ugyanaz a fázis
következik, a hullám térbeli periódusa, a hullámhossz. Jele: λ.

A harmonikus hullám terjedési sebességén a fázis terjedésének sebességét értjük.
Nagyságát megkapjuk, ha a periódushosszat ( a fázis T idı alatt megtett útját ) osztjuk a
megtételéhez szükséges idővel,a periódusidővel. Jele: c.





Indítsunk egy rugalmas kötélen transzverzális hullámokat úgy, hogy a kezdıpont
kitérésének irányát állandóan változtatjuk. Ha a kötelet egy keskeny, függőleges helyzető
résen vezetjük keresztül, azt tapasztaljuk, hogy a rés után a kötél minden pontja függőleges irányban rezeg tovább. így a rés polarizálta a transzverzális hullámot és longitudinális hullám lett belőle. Ezt a jelenséget hullámpolarizációnak nevezzük.

Ha egy megfigyelt pont rezgésének iránya mindig egyazon egyenesbe esik, lineárisan
poláros hullámról beszélünk.

Ha egy megfigyelt pont rezgésének iránya egyenletesen körbe jár, akkor cirkulárisan
poláros a hullám.

A felületi, térbeli hullámok és az interferencia: Ha a víz felszínét egy pontjában
periodikusan ütögetjük, akkor körhullámok alakulnak ki. Az azonos fázisú pontok, a
forrással koncentrikus körök, ezek alkotják a körhullámok hullámfrontjait. Ha a víz
felszínét nem csak egy pontban, hanem egy szakasz mentén periodikusan ütögetjük, akkor
vonalhullámok alakulnak ki. Térben gömbhullámokról és síkhullámokról is beszélhetünk.

A szuperpozíció különleges esetével fogunk foglakozni: amikor a hullámok találkozása
maradandó, jól megfigyelhető mintázatot hoz létre a hullámtérben. Ez akkor jön létre, ha a
tér egyes pontjaiban a találkozó hullámok fáziskülönbsége időben állandó, szaknyelven
szólva, ha a találkozó hullámok koherensek. Ilyet tudunk előállítani úgy, hogy például két
egymáshoz rögzített tővel rezegtetjük a víz felszínét.

Általában az interferencia észlelhetőségének feltétele az, hogy a két hullámforrás
fáziskülönbsége időben állandó. Ez az ún. koherencia-feltétel.

Ekkor a találkozó hullámoknak azonos a rezgésszámuk, de a vízfelület különböz
pontjaiba általában különböző fázissal érkeznek a két hullámforrás irányából. A felület
egyes pontjaiba tartósan erős hullámzást, mást pontokban gyöngülést, vagy a hullámzás
megszűnését (kioltását) figyelhetjük meg. Az ilyen tartósan megmaradó
hullámszuperpozíciót interferenciának nevezzük.

Két egy pontba érkező hullám akkor erısíti egymást maximális mértékben, ha a
találkozás helyén rezgéseik azonos fázisban vannak.

Ha viszont az útkülönbség a félhullámhossz, vagy annak páratlan számú többszöröse, a
két beérkező hullám maximális mértékben gyengíti ( azonos amplitúdók esetén kioltja )
egymást.

A maximális erısítés feltétele:





A maximális gyengítés feltétele:





Elhajlás, A Huygens-Fresnel-féle elv: Egy hullám egy széles résen való áthaladása
során úgy tőnik, hogy a hullám egyenes vonalban terjed tovább. (Például egy nyitott ajtón
keresztül a hanghullám). Ha viszont szűkítjük a rést a hullám elhajlani látszik, és hogyha a
rés még jobban összeszűkül, a hullám elhajlik. Ahogy a rés mérete a hullámhossz
nagyságához közeledik. Ekkor a rés után a hullám, olyan alakot ölt, mint ha a rés lenne egy pontszerő test által létrehozott körhullám forrása.

A széles és a keskeny rés látszólag egészen különböző viselkedése mögött tehát
ugyanaz a törvény húzódik meg: Egy hullám fázisfelületének minden pontja elemi ( vagy
másodlagos ) hullámforrás, és az ezekből kiinduló elemi hullámoknak a szuperpozíciója
adja a tér valamely pontjában észlelhető hullámkitérést. A hullámfront minden pontjából
elemi körhullámok (térben gömbhullámok) indulnak ki. Ezen elemi hullámok
interferenciája adja az új hullámfrontot.

Hullámok visszaverődése, törése: A beeső és visszavert hullámok azonos szöget
zárnak be a beesési merılegessel ( az új közeg határára emelt merıleges egyenes), más
szóval a beesési szög egyenlő a visszaverıdési szöggel.

Ha a két közegben különböző sebességgel terjed a hullám, akkor a hullám megtörik.

Megállapítható, hogy a beesési szög ( α ) és a törési szög ( β ) szinuszainak hányadosa
állandó. Ezt az állandót, amely csak a két közeg minőségétől függ, a második közegnek az
elsőre vonatkozó törésmutatójának nevezzük. Jele:n.


































Állóhullámok: Egy kifeszített húrt olyan rezgésben lehet tartani, amelyben egyes
részecskéinek rezgésamplitúdója különböző, de időben állandó nagyságú.Ilyenkor a test
felbontható olyan tartományokra, amelyeken belül a részecskék mindegyike azonos
fázisban rezeg. Az egymással szomszédos tartományok pontjai ellentétes fázisban rezegnek. A hullámkép érdekessége, hogy a rezgésállapot semmilyen irányban nem terjed. Ezért ezt a jelenséget állóhullámnak hívjuk.

Az állóhullám legnagyobb amplitúdójú pontjait duzzadóhelyeknek, a nyugalomban
lévő helyeit csomópontoknak hívjuk. Az állóhullám két azonos frekvenciájú, ellentétes
irányba haladó hullám interferenciája. Állóhullámok csak olyan frekvenciákon jöhetnek
létre, amelyek során kialakuló hulláminterferencia eleget tesz annak a követelménynek,
hogy a rögzített végeken éppen csomópontok jönnek létre. Csak olyan frekvenciákon jöhet
létre amelyeknél kiadódó félhullám egész számszor fér rá a húrra.

Az első lehetséges frekvencia amelynél állóhullám jöhet létre az ún. alapfrekvencia.



ahol L a húr hossza.

Az ezt követő állóhullámok az alapfrekvencia egész számú többszörösei, amiket
felharmonikusoknak nevezünk:

   A hallószervünk által felfogható mechanikai rezgéseket hangnak nevezzük.
A hang terjedési sebessége a rezonanciából hozott adataiból könnyen meghatározható.
A hang normál állapotban, levegőben 332 m/s sebességgel terjed. A terjedéséhez közvetítő szükséges. (vízben 1400 m/s, acélban 5000 m/s).
A hang magasságát kizárólag a hang rezgésszáma határozza meg. Azt azonban, hogy
melyik magasabb a másiknál, a rezgésszámaik hányadosa adja. Pl.: 1 : 2 rezgésszámarányú hangközt oktávnak nevezünk.

A kifeszített húron végzett kísérletünkbıl arra a következtetésre jutottunk, hogy a hang
összetett rezgés: Az alaphangokon kívül a felharmonikusokat is tartalmazza. Ezeket
felhangoknak nevezzük. A színezetét tehát az alaphanggal együtt megszólaló felhangok
keveréke (amplitúdóik aránya) határozza meg.

A Doppler-effektus: Ha a közeledő autó hangját figyeljük, az mind egyre magasabb,
míg a távolodó autó hangja egyre mélyebb lesz. Ez azért figyelhető meg, mert a közeledő
hanghullámok egymásra halmozódnak, míg a távolodó hullámok megnyúlnak, így
hullámhosszuk is nő, illetve csökken. Ez a Doppler-effektus.

Ha az észlelő u sebességgel közeledik, a frekvencia:




a forrás sebessége v.





ha az észlelő u sebességgel távolodik.