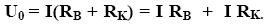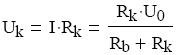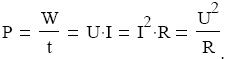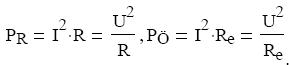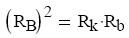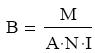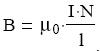Physical blog

   Vizsgáljuk meg, hogy egy hosszú fémes vezetőn hogyan függ az áram erőssége a két
végpont közötti feszültségtől. Mérési eredményeink egyenes arányosságot mutatnak. Tehát U/I = állandó. Az állandó értéke független a fogyasztóra kapcsolt feszültségtıl vagy a rajta átfolyó áramtól, így kizárólag az adott fogyasztóra jellemző. Neve: elektromos ellenállás, jele: R, mértékegysége Ohm, jele:


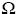
Egy vezeték ellenállása akkor 1 Ohm, ha 1 V feszültség hatására 1 A erősségű áram halad
benne.

Állandó U feszültségű telep esetén az áramkörben bárhol ugyanakkora az áramerősség.
Ez azt jelenti, hogy mozgása a vezetőben egyenletes, pedig az állandó feszültség miatt
kialakuló homogén elektromos tér gyorsítja a töltéseket. Fel kell tételeznünk tehát egy belső fékező erőt, amelynek hatására a töltések mozgása a fémben a súrlódás áramlásához hasonlóan megy végbe. Ez a belső, anyagszerkezeti jelenségekre visszavezethető hatás jellemezhet a vezető ellenállásával.

Fémes vezetők ellenállása, fajlagos ellenállás:
Mérjük meg különböző hosszúságú, keresztmetszető, ill. anyagi minıségű fémhuzalok
ellenállását. Állandó feszültség esetén a következő arányosság állapítható meg: I ~ A/l, ahol A a huzal keresztmetszete, l a hossza. Ezt felhasználva, a huzal ellenállására a következő összefüggés írható fel: R = U/I = ρ · l/A, ahol ρ az anyagi minıségtől függő arányossági tényező, a fajlagos elektromos ellenállás, mértékegysége: Ohm m.

Az ellenállás hőmérséklettől való függése
A fémes vezetőkben állandó hőmérsékleten és állandó feszültség esetén az ún. vezetési
elektronok átlagos állandó sebességgel szállítják az elektromos töltést. A hőmérséklet
növekedésével az elektronok egyre gyakrabban ütköznek a hőmozgást végző ionokba, emiatt átlagos sebességük lecsökken, így a fém ellenállása megnő.

Az elektronok átlagos sebessége (amellyel a vezetésben részt vesznek) lényegesen
növelhető – azaz lényegesen lecsökkenthető az ellenállás -, ha a fémrács ionjainak hőmozgása lecsökken. 0 Kelvinhez közeli hőmérsékleten, minden idegen szennyező atomtól mentes, tiszta fémes vezető ellenállása a nullához tart (szupravezetés). Grafit esetén viszont kevés elektron vesz részt a vezetésben alacsony hőmérsékleten.
A hőmérséklet emelésével jelentősen megnő a vezetésben részt vevő elektronok száma, vagyis ilyenkor a hőmozgás „delokalizálja” a grafit kristályrácsának elektronjait, ami oda vezet, hogy az áram megnő, tehát az elektromos ellenállás lecsökken.

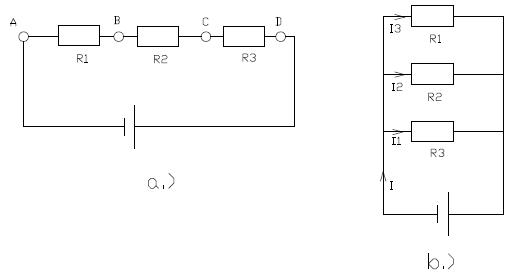
Ellenállások soros kapcsolása
Egy áramkörben az ellenállások kapcsolása két pont között soros, ha a két pont között
nincs semmiféle elágazás.
Egy sorosan kapcsolt ellenállásokat tartalmazó áramkör eredő ellenállásán azt az
ellenállást értjük, amelyet ugyanarra az U0 feszültségű telepre kapcsolva, ugyanaz az I
áramerısség jön létre.



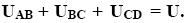
Alkalmazva az egyenletre Ohm törvényét:



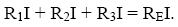
Osztva az áramerısséggel, megkapjuk az eredő ellenállásra vonatkozó összefüggést:




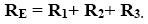
Ellenállások párhuzamos kapcsolása

párhuzamos az ellenállások kapcsolása, ha a csatlakozási pontok egy-egy oldalon
azonos potenciálon vannak.

Kirchoff I. törvénye – csomóponti törvény:
Egy hálózat minden elágazási pontjára (csomópontjára) igaz, hogy a beérkező és a
kifolyó áramok elıjeles összege zérus. Σ I(also index:K) = 0.
A csomóponti törvény a töltésmegmaradás tételének következménye.

Kapcsoljunk párhuzamosan három ellenállást . Alkalmazzuk az adott áramkörre Kirchoff I. törvényét.



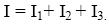
Az áramerősségekre kapott egyenletet alakítsuk át az Ohm-törvény felhasználásával, így
meghatározhatjuk az eredő ellenállás értékét:





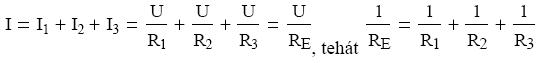
Ez azt mutatja, hogy párhuzamos kapcsolás esetén az egyes ellenállásokon folyó áramok
az ellenállások értékével fordítottan arányosak.

   Egy áramkörben a feszültségforrás, vagy telep feszültségén a forrásfeszültséget, vagy
elektromotoros erőt értjük. Jele: U0.
Ha az áram átfolyik a telepen is, akkor azt tapasztaljuk, hogy annak ellenállása van. Ez
az ellenállást belsı ellenállásnak hívjuk. Tehát az RK külsı ellenállás és az RB belsı
ellenállás határozza meg az áramkörben kialakuló áram erısségét.



Ez a kifejezés az Ohm-törvény teljes áramkörre vonatkozó alakja, amelyben RB az
összes külsı ellenállás eredıjét jelenti. Eredményünk alapján Kirchoff II. törvénye, a
huroktörvény is megadható általános alakban:

Egy hálózat bármely zárt hurkot alkotó részében az ellenállásokra jutó feszültségek
összege egyenlı a körben lévı elektromotoros erık összegével:
Σ I(alsó index:J) R(alsó index:J) = Σ U(alsó index:0).

Ahol RJ a telepek belsıellenállását is tartalmazza. Ha kiegészítjük a törvényt Kirchoff I.
törvényével, akkor megkapjuk, hogy egy hálózat bármely csomópontjába befutó áramok
elıjeles összege nulla: Σ I(alsó index:J) = 0.

Az eddigiekbıl kitőnik, hogy az RK fogyasztóra csak IRK = UK feszültség jut,
amelynek a neve kapocsfeszültség. A kapocsfeszültség a terheléstıl függıen jóval kisebb is
lehet a forrásfeszültségnél, ugyanis:





Eredményünkbıl az is látszik, hogy a telepbıl RK = 0 esetén lesz az áram maximális. Ez
az ún. rövidzárási áram: Imax = U(alsó index:0) / R(alsó index:B).

   Áram hatására a különböző anyagú és minőségű vezetők különböző mértékben
melegszenek. Azonos keresztmetszetű és hosszúságú vezetők esetén a legnagyobb fajlagos ellenállású drót melegszik jobban. Az elektromos áram hőt termel, amelynek nagysága a fogyasztó adataitól is függ. Ez a Joule-féle hő. Ha leírjuk a munkavégzést, amelyet az elektromos tér végez A-B pont között, miközben Q töltés halad át t idő alatt: W = UAB Q.

Ez a kifejezés Ohm-törvényének segítségével átalakítható:





Az elektromos munkára kapott kifejezésből definiálható az R ellenállású fogyasztó által
felvett teljesítmény:






Az elektromos hálózatra jellemző a munkavégzés hasznosságára vonatkozó hatásfok:
η = PR / PÖ, ahol PR a fogyasztó által felvett teljesítmény, PÖ a feszültségforrás által
leadott összes teljesítmény:






Tapasztalatok azt igazoljál, hogy egy nem ideális telepből kivehető teljesítmény a külső
ellenállás függvényében akkor maximális, ha Rb = Rk.
Azt mondhatjuk, hogy akkor vehetünk ki egy telepből maximális teljesítményt, ha a külső és a belső ellenállás megegyezik, vagyis illesztve vannak. Minden más (kisebb) teljesítményértékhez két Rk érték tartozik. Érdekes, hogy bármely összetartozó Rk értékpár mértani közepe a belső ellenállást adja meg:

   Ha egy mágnest feldarabolunk, minden darabjának megmarad a lét pólusa, tehát
mágneses monopólus nem létezik.
Ha az iránytű fölött az iránytűvel megegyező irányban kifeszítünk egy vezetéket, és
áram alá helyezzük azt, az iránytű kitér a drótra merőleges irányban.(Oersted-kísérlet).
Ha kifeszítünk két drótot egymással párhuzamosan, amikben áram folyik, azok taszítani,
vagy vonzani fogják egymást, attól függően, hogy azonos, vagy ellentétes irányban folyik az áram a két vezetőben.
Ezekből a jelenségekből azt vonhatjuk le, hogy akár permanens mágnest, akár áramjárta
vezetőt használunk, mágneses mező alakul ki körülöttük, amely közvetíti az erőhatást a
mágnesek, illetve az áramjárta vezetők között. Ez a mező akkor is jelen van, ha nincs ott
másik mágnes, vagy áramjárta vezető. Ezt a mágneses térre jellemző mennyiséget mágneses indukciónak nevezzük.


A mágneses indukció
Tudjuk, hogy az iránytű kétpólusú mágnes, tehát helyettesíthető egy olyan tekerccsel,
amelyben áram folyik. Ha egy tekercsbe áramot vezetünk, az előbbiek szerint beáll egy
egyensúlyi helyzetbe, ami jelen esetben az déli-északi irány lesz. A mágneses
indukcióvektor nagyságát, pedig úgy kapjuk meg, hogy megmérjük a tekercs egyensúlyi
helyzetéből 90 fokkal elfordított helyzetéhez szükséges forgatónyomaték nagyságát, amit
elosztunk a próbatekercs felületének, menetszámának, és a benne folyó áram erősségének
szorzatával. A mágneses indukcióvektor iránya az egyensúlyi helyzetbe beállt próbatekercs déli pólusából az északi pólusa felé mutató irány. Jele: B, mértékegysége: N/Am = 1 Tesla = T.




ahol A a felület, N a menetszám, I az áramerősség, M a forgatónyomaték.
Mivel a mágneses tér nem fejt ki erőt a vele párhuzamos áramjárta vezetőre,
átrendezzük egy kicsit a képletünket ennek megfelelően. Vegyünk egy áramjárta vezetőt, ami merőlegesen helyezkedi el B indukcióvektorra, akkor az erőhatás merőleges lesz az
indukcióvektorra, és az áramjárta vezetıben az áramerősségre is. (Jobbkéz szabály).












Általánosítva az előbbi formulánkat: F = BI l cos(alfa) , ahol α a vezető és a B
indukcióvonalakkal bezárt szög, l pedig a vezető hossza, I az áramerősség.
Ha egy Q töltés sebességét vizsgáljuk egy l hosszúságú vezetőn amin t idı alatt fut
végig, a képletünk a következıképpen alakul: l = vt, I = Q/t,
F= Q×v×B×sin(alfa), ahol α a B indukcióvonalaknak a sebességvektorral bezárt szöge.
 A mágneses térben v sebességgel mozgó Q töltésű részecskére ható erő eszerint merőleges v-re és B-re, velük jobbrendszert alkot. Ez az erı a mágneses Lorentz-erő.
A Lorentz-erő csak a sebesség irányát változtathatja meg, a nagyságát nem, merőleges lévén a sebességre.


Mágneses indukcióvonalak
Lényeges különbség az elektrosztatikus térhez képest, hogy az indukcióvonalaknak
nincs kezdetük és végük, hanem önmagukba záródnak. Ha egy mágnes köré vasreszeléket
szórunk, akkor azok az indukcióvonalak irányába rendeződnek, így azokat szabad szemmel is láthatjuk. Az indukcióvektor az indukcióvonal bármely pontjában érintő irányú.
Egy adott egységnyi felületen átfutó indukcióvonalak száma a mágneses fluxus. Jele: Φ,
mértékegysége: (égyzetméter) T = Weber = Wb. Φ = BA.
Ha a mágneses mez felülete nem homogén, akkor azt felosztjuk egységnyi darabokra
és azok összességét vesszük a nem homogén mágneses mezı fluxusának:Ha a mágneses mező felülete nem homogén, akkor azt felosztjuk egységnyi darabokra és azok összességét vesszük a nem homogén mágneses mező fluxusának: ΣB(alsó indexben: n)  (delta) A. Mivel az indukcióvonalak önmagukban záródó görbék, zárt felületre vonatkozóan az indukciófluxus nulla, ami azt fejezi ki, ha egy indukcióvonal a zárt felületen bement,
akkor ki is jön belıle.


Tekercs mágneses tere
Ha megvizsgáljuk, mitől függ a tekercs belsejében kialakuló mágneses tér indukciója,
azt látjuk, hogy az a tekercs I áramától, N menetszámától, és a tekercs l hosszúságától függ, viszont nem függ a keresztmetszettől, így:




ahol μ0 a vákuum permeabilitása, értéke:





Egyenes vezető mágneses tere
A tekercshez hasonlóan megvizsgáljuk a hosszú egyenes vezető mágnese terét is.





ahol I a vezetékben folyó áram, r pedig a vizsgált pont vezetőtől mért távolsága.

 Mozgási indukció
Mozgassunk l hosszúságú fémrudat B indukciójú mágneses térben úgy, hogy a l
merőleges legyen B-re és v-re. Ekkor a fémrúd belsejében lévı szabad töltésekre rúdirányban hat a Lorentz-erı, és töltésmegosztást eredményez. Az így létrejövő E elektromos tér által a töltésekre kifejtett erő a Lorentz-erıvel ellentétes.
A töltésmegosztás addig tart, amíg ez a két hatás egyensúlyba kerül: QvB=QE, amiből
E = vB, vagyis a rúdban homogén indukált elektromos mező jön létre, tehát a fezsültség az l hosszúságú rúd végei között: U = vBl.
Amennyiben v és B nem merőlegesek egymásra, hanem α szöget zárnak be, akkor a
képlet: U = vBl sinα. Ezt az összefüggést Neumann-féle törvénynek nevezzük.

Lenz-törvény
Az imént láttuk, hogy ha B indukciójú mágneses mezőben egy l hosszúságú rudat B-re
és l-re egyaránt merőleges irányban v sebességgel mozgatunk, akkor végei között: U=Bvl.
Ha áram is folyik a rúdban, I = U/R = Bvl/R, mivel zárt az áramkör.
Másképp kifejezve: F = BIl = B2l2v/R.
Az indukált feszültség által létrehozott áram iránya olyan, hogy hatásával gátolja az őt
létrehozó mozgást. Ez Lenz törvénye.
Ez a törvény voltaképpen az energia-megmaradás törvényét fejezi ki. Ezért nem tud az
indukált áram hatására a rudunk gyorsulva elmozdulni.