rezgési energia térben terjed tova.
Laza rugó egyik végét rögzítsük, a másik végét pedig hirtelen rántsuk meg
hosszirányban. Azt tapasztaljuk, hogy az így létrehozott deformáció végigfut a rugón, majd a rögzített cégérıl visszaverıdik. Ugyanezt tapaszaljuk, ha keresztirányban ráütünk. Ekkor egy ’völgy’ fut végig a rugón. Ha jobban megfeszítjük a rugót, akkor gyorsabban terjed a deformáció, ha kevésbé feszítjük meg, akkor lassabban.
Ha a rugó két végéről egyszerre indítjuk a deformációt, azok mintegy „áthaladnak”
egymáson. A találkozás helyén lévő pontok mind a két deformációnak eleget tesznek, azaz
a két kitérés összeadódik, szuperponálódik. Egy testen két rezgés egyidejű megvalósítását, azaz a két rezgés zavartalan összetételét szuperpozíciónak nevezzük.
Az a legkisebb távolság, amely után (az adott idıpillanatban) újra ugyanaz a fázis
következik, a hullám térbeli periódusa, a hullámhossz. Jele: λ.
A harmonikus hullám terjedési sebességén a fázis terjedésének sebességét értjük.
Nagyságát megkapjuk, ha a periódushosszat ( a fázis T idı alatt megtett útját ) osztjuk a
megtételéhez szükséges idővel,a periódusidővel. Jele: c.
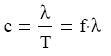
Indítsunk egy rugalmas kötélen transzverzális hullámokat úgy, hogy a kezdıpont
kitérésének irányát állandóan változtatjuk. Ha a kötelet egy keskeny, függőleges helyzető
résen vezetjük keresztül, azt tapasztaljuk, hogy a rés után a kötél minden pontja függőleges irányban rezeg tovább. így a rés polarizálta a transzverzális hullámot és longitudinális hullám lett belőle. Ezt a jelenséget hullámpolarizációnak nevezzük.
Ha egy megfigyelt pont rezgésének iránya mindig egyazon egyenesbe esik, lineárisan
poláros hullámról beszélünk.
Ha egy megfigyelt pont rezgésének iránya egyenletesen körbe jár, akkor cirkulárisan
poláros a hullám.
A felületi, térbeli hullámok és az interferencia: Ha a víz felszínét egy pontjában
periodikusan ütögetjük, akkor körhullámok alakulnak ki. Az azonos fázisú pontok, a
forrással koncentrikus körök, ezek alkotják a körhullámok hullámfrontjait. Ha a víz
felszínét nem csak egy pontban, hanem egy szakasz mentén periodikusan ütögetjük, akkor
vonalhullámok alakulnak ki. Térben gömbhullámokról és síkhullámokról is beszélhetünk.
A szuperpozíció különleges esetével fogunk foglakozni: amikor a hullámok találkozása
maradandó, jól megfigyelhető mintázatot hoz létre a hullámtérben. Ez akkor jön létre, ha a
tér egyes pontjaiban a találkozó hullámok fáziskülönbsége időben állandó, szaknyelven
szólva, ha a találkozó hullámok koherensek. Ilyet tudunk előállítani úgy, hogy például két
egymáshoz rögzített tővel rezegtetjük a víz felszínét.
Általában az interferencia észlelhetőségének feltétele az, hogy a két hullámforrás
fáziskülönbsége időben állandó. Ez az ún. koherencia-feltétel.
Ekkor a találkozó hullámoknak azonos a rezgésszámuk, de a vízfelület különböz
pontjaiba általában különböző fázissal érkeznek a két hullámforrás irányából. A felület
egyes pontjaiba tartósan erős hullámzást, mást pontokban gyöngülést, vagy a hullámzás
megszűnését (kioltását) figyelhetjük meg. Az ilyen tartósan megmaradó
hullámszuperpozíciót interferenciának nevezzük.
Két egy pontba érkező hullám akkor erısíti egymást maximális mértékben, ha a
találkozás helyén rezgéseik azonos fázisban vannak.
Ha viszont az útkülönbség a félhullámhossz, vagy annak páratlan számú többszöröse, a
két beérkező hullám maximális mértékben gyengíti ( azonos amplitúdók esetén kioltja )
egymást.
A maximális erısítés feltétele:
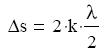
A maximális gyengítés feltétele:
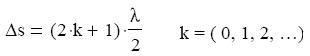
Elhajlás, A Huygens-Fresnel-féle elv: Egy hullám egy széles résen való áthaladása
során úgy tőnik, hogy a hullám egyenes vonalban terjed tovább. (Például egy nyitott ajtón
keresztül a hanghullám). Ha viszont szűkítjük a rést a hullám elhajlani látszik, és hogyha a
rés még jobban összeszűkül, a hullám elhajlik. Ahogy a rés mérete a hullámhossz
nagyságához közeledik. Ekkor a rés után a hullám, olyan alakot ölt, mint ha a rés lenne egy pontszerő test által létrehozott körhullám forrása.
A széles és a keskeny rés látszólag egészen különböző viselkedése mögött tehát
ugyanaz a törvény húzódik meg: Egy hullám fázisfelületének minden pontja elemi ( vagy
másodlagos ) hullámforrás, és az ezekből kiinduló elemi hullámoknak a szuperpozíciója
adja a tér valamely pontjában észlelhető hullámkitérést. A hullámfront minden pontjából
elemi körhullámok (térben gömbhullámok) indulnak ki. Ezen elemi hullámok
interferenciája adja az új hullámfrontot.
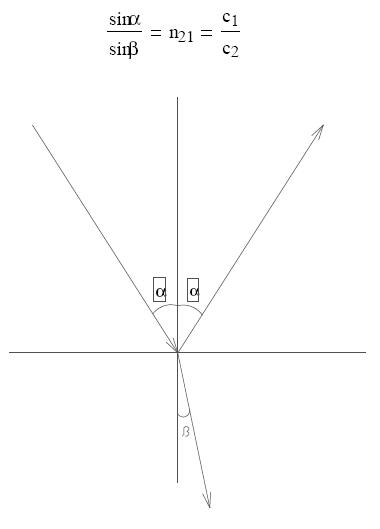
Hullámok visszaverődése, törése: A beeső és visszavert hullámok azonos szöget
zárnak be a beesési merılegessel ( az új közeg határára emelt merıleges egyenes), más
szóval a beesési szög egyenlő a visszaverıdési szöggel.
Ha a két közegben különböző sebességgel terjed a hullám, akkor a hullám megtörik.
Megállapítható, hogy a beesési szög ( α ) és a törési szög ( β ) szinuszainak hányadosa
állandó. Ezt az állandót, amely csak a két közeg minőségétől függ, a második közegnek az
elsőre vonatkozó törésmutatójának nevezzük. Jele:n.
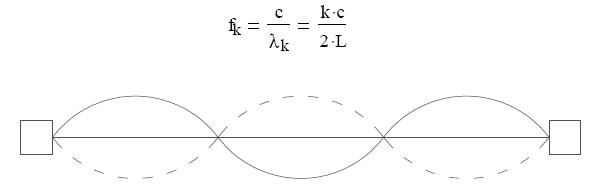
Állóhullámok: Egy kifeszített húrt olyan rezgésben lehet tartani, amelyben egyes
részecskéinek rezgésamplitúdója különböző, de időben állandó nagyságú.Ilyenkor a test
felbontható olyan tartományokra, amelyeken belül a részecskék mindegyike azonos
fázisban rezeg. Az egymással szomszédos tartományok pontjai ellentétes fázisban rezegnek. A hullámkép érdekessége, hogy a rezgésállapot semmilyen irányban nem terjed. Ezért ezt a jelenséget állóhullámnak hívjuk.
Az állóhullám legnagyobb amplitúdójú pontjait duzzadóhelyeknek, a nyugalomban
lévő helyeit csomópontoknak hívjuk. Az állóhullám két azonos frekvenciájú, ellentétes
irányba haladó hullám interferenciája. Állóhullámok csak olyan frekvenciákon jöhetnek
létre, amelyek során kialakuló hulláminterferencia eleget tesz annak a követelménynek,
hogy a rögzített végeken éppen csomópontok jönnek létre. Csak olyan frekvenciákon jöhet
létre amelyeknél kiadódó félhullám egész számszor fér rá a húrra.
Az első lehetséges frekvencia amelynél állóhullám jöhet létre az ún. alapfrekvencia.
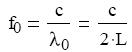
ahol L a húr hossza.
Az ezt követő állóhullámok az alapfrekvencia egész számú többszörösei, amiket
felharmonikusoknak nevezünk: